Algos算法教程

Rust作为一门现代化的系统编程语言，拥有与C/C++类似的性能，同时又能做非常底层的性能优化，因此非常适合写算法和leetcode。

Algos 算法教程涵盖了各种常用算法和数据结构的代码实现，以及leetcode题解，同时对于相关算法还提供了中文文档和注释，可以帮助大家更好、更快的学习。

关于算法

算法，一个高大上的词汇，在计算机领域也绝对是凡人的禁忌，但是其实算法又没那么神秘，我们在写代码时，无时无刻都在与算法打交道，只是绝大部分算法我们无法感知到而已，因为这些算法已经很好的被包装在其它库中，我们只需要输入数据然后调用它获得输出数据即可，因此这就引出了算法的基本定义：

计算机算法是以一步接一步的方式来详细描述计算机如何将输入转化为所要求的输出的过程，或者说，算法是对计算机上执行的计算过程的具体描述。（以上内容摘抄自百度百科），简单点说计算机算法就是将输入转化为所要求的输出过程。

既然只要调用别人的算法库即可完成任务，我们为什么要学习算法呢？原因很简单：面试需要。哈哈，开个玩笑，当然面试很重要，但是提升自己的能力也很重要，学习算法往往能提升我们对于代码的深层次理解和认识，你会知道为何要优化代码，该如何优化代码，甚至在真的需要你手撸算法时，心中也有一个明确的思路：我该选择哪个算法，而不是一片茫然，只知道用遍历的方式来完成任务。

所以现在开始我们的算法之旅吧， 本章重点呈现各种常用算法的Rust实现，大部分章节都会链接一篇讲解该算法的文章。

Rust 语言学习

如果大家熟悉算法，但是对于 Rust 语言还不够熟悉，可以看看 Rust语言圣经，它绝对是目前最优秀的 Rust 中文开源教程。

社区贡献者

我们深知自身水平的局限性，因此非常欢迎各路大神加入进来，共同打造这门未来可以在中国乃至全世界都排得上号的算法教程！

排序算法

所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视，尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范，要得到一个符合实际的优秀算法，得经过大量的推理和分析。

冒泡排序

#![allow(unused)]
fn main() {
pub fn bubble_sort<T: PartialOrd>(arr: &mut [T]) {
    if arr.len() <= 1 {
        return;
    }

    let size = arr.len();
    for i in 0..(size - 1) {
        // 标记当前循环是否发生元素交换
        let mut swapped = false;

        // 最后i个元素已经排好了顺序
        for j in 1..(size - i) {
            if arr[j - 1] > arr[j] { 
                arr.swap(j - 1, j);
                swapped = true;
            }
        }

        // 如果当前循环没有发生元素交换，说明数组已经有序
        if !swapped {
            break;
        }
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_empty_vec() {
        let mut empty_vec: Vec<String> = vec![];
        bubble_sort(&mut empty_vec);
        assert_eq!(empty_vec, Vec::<String>::new());
    }

    #[test]
    fn test_number_vec() {
        let mut vec = vec![7, 49, 73, 58, 30, 72, 44, 78, 23, 9];
        bubble_sort(&mut vec);
        assert_eq!(vec, vec![7, 9, 23, 30, 44, 49, 58, 72, 73, 78]);
    }

    #[test]
    fn test_string_vec() {
        let mut vec = vec![
            String::from("Bob"),
            String::from("David"),
            String::from("Carol"),
            String::from("Alice"),
        ];
        bubble_sort(&mut vec);
        assert_eq!(
            vec,
            vec![
                String::from("Alice"),
                String::from("Bob"),
                String::from("Carol"),
                String::from("David"),
            ]
        );
    }
}
}

桶排序

#![allow(unused)]
fn main() {
/// Sort a slice using bucket sort algorithm.
///
/// Time complexity is `O(n + k)` on average, where `n` is the number of elements,
/// `k` is the number of buckets used in process.
///
/// Space complexity is `O(n + k)`, as it sorts not in-place.
pub fn bucket_sort(arr: &[usize]) -> Vec<usize> {
    if arr.is_empty() {
        return vec![];
    }

    let max = *arr.iter().max().unwrap();
    let len = arr.len();
    let mut buckets = vec![vec![]; len + 1];

    for x in arr {
        buckets[len * *x / max].push(*x);
    }

    for bucket in buckets.iter_mut() {
        super::insertion_sort(bucket);
    }

    let mut result = vec![];
    for bucket in buckets {
        for x in bucket {
            result.push(x);
        }
    }

    result
}

#[cfg(test)]
mod tests {
    use super::super::is_sorted;
    use super::*;

    #[test]
    fn empty() {
        let arr: [usize; 0] = [];
        let res = bucket_sort(&arr);
        assert!(is_sorted(&res));
    }

    #[test]
    fn one_element() {
        let arr: [usize; 1] = [4];
        let res = bucket_sort(&arr);
        assert!(is_sorted(&res));
    }

    #[test]
    fn already_sorted() {
        let arr: [usize; 3] = [10, 9, 105];
        let res = bucket_sort(&arr);
        assert!(is_sorted(&res));
    }

    #[test]
    fn basic() {
        let arr: [usize; 4] = [35, 53, 1, 0];
        let res = bucket_sort(&arr);
        assert!(is_sorted(&res));
    }

    #[test]
    fn odd_number_of_elements() {
        let arr: Vec<usize> = vec![1, 21, 5, 11, 58];
        let res = bucket_sort(&arr);
        assert!(is_sorted(&res));
    }

    #[test]
    fn repeated_elements() {
        let arr: Vec<usize> = vec![542, 542, 542, 542];
        let res = bucket_sort(&arr);
        assert!(is_sorted(&res));
    }
}
}

鸡尾酒排序

#![allow(unused)]
fn main() {
pub fn cocktail_shaker_sort<T: Ord>(arr: &mut [T]) {
    let len = arr.len();

    if len == 0 {
        return;
    }

    loop {
        let mut swapped = false;

        for i in 0..(len - 1).clamp(0, len) {
            if arr[i] > arr[i + 1] {
                arr.swap(i, i + 1);
                swapped = true;
            }
        }

        if !swapped {
            break;
        }

        swapped = false;

        for i in (0..(len - 1).clamp(0, len)).rev() {
            if arr[i] > arr[i + 1] {
                arr.swap(i, i + 1);
                swapped = true;
            }
        }

        if !swapped {
            break;
        }
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        let mut arr = vec![5, 2, 1, 3, 4, 6];
        cocktail_shaker_sort(&mut arr);
        assert_eq!(arr, vec![1, 2, 3, 4, 5, 6]);
    }

    #[test]
    fn empty() {
        let mut arr = Vec::<i32>::new();
        cocktail_shaker_sort(&mut arr);
        assert_eq!(arr, vec![]);
    }

    #[test]
    fn one_element() {
        let mut arr = vec![1];
        cocktail_shaker_sort(&mut arr);
        assert_eq!(arr, vec![1]);
    }

    #[test]
    fn pre_sorted() {
        let mut arr = vec![1, 2, 3, 4, 5, 6];
        cocktail_shaker_sort(&mut arr);
        assert_eq!(arr, vec![1, 2, 3, 4, 5, 6]);
    }
}
}

梳排序

#![allow(unused)]
fn main() {
pub fn comb_sort<T: Ord>(arr: &mut [T]) {
    let mut gap = arr.len();
    let shrink = 1.3;
    let mut sorted = false;

    while !sorted {
        gap = (gap as f32 / shrink).floor() as usize;
        if gap <= 1 {
            gap = 1;
            sorted = true;
        }
        for i in 0..arr.len() - gap {
            let j = i + gap;
            if arr[i] > arr[j] {
                arr.swap(i, j);
                sorted = false;
            }
        }
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn descending() {
        //descending
        let mut ve1 = vec![6, 5, 4, 3, 2, 1];
        comb_sort(&mut ve1);
        for i in 0..ve1.len() - 1 {
            assert!(ve1[i] <= ve1[i + 1]);
        }
    }

    #[test]
    fn ascending() {
        //pre-sorted
        let mut ve2 = vec![1, 2, 3, 4, 5, 6];
        comb_sort(&mut ve2);
        for i in 0..ve2.len() - 1 {
            assert!(ve2[i] <= ve2[i + 1]);
        }
    }
}
}

计数排序

#![allow(unused)]
fn main() {
/// In place counting sort for collections of u32
/// O(n + maxval) in time, where maxval is the biggest value an input can possibly take
/// O(maxval) in memory
/// u32 is chosen arbitrarly, a counting sort probably should'nt be used on data that requires bigger types.

pub fn counting_sort(arr: &mut [u32], maxval: usize) {
    let mut occurences: Vec<usize> = vec![0; maxval + 1];

    for &data in arr.iter() {
        occurences[data as usize] += 1;
    }

    let mut i = 0;
    for (data, &number) in occurences.iter().enumerate() {
        for _ in 0..number {
            arr[i] = data as u32;
            i += 1;
        }
    }
}

use std::ops::AddAssign;
/// Generic implementation of a counting sort for all usigned types
pub fn generic_counting_sort<T: Into<u64> + From<u8> + AddAssign + Copy>(
    arr: &mut [T],
    maxval: usize,
) {
    let mut occurences: Vec<usize> = vec![0; maxval + 1];

    for &data in arr.iter() {
        occurences[data.into() as usize] += 1;
    }

    // Current index in output array
    let mut i = 0;

    // current data point, necessary to be type-safe
    let mut data = T::from(0);

    // This will iterate from 0 to the largest data point in `arr`
    // `number` contains the occurances of the data point `data`
    for &number in occurences.iter() {
        for _ in 0..number {
            arr[i] = data;
            i += 1;
        }

        data += T::from(1);
    }
}

#[cfg(test)]
mod test {
    use super::super::is_sorted;
    use super::*;

    #[test]
    fn counting_sort_descending() {
        let mut ve1 = vec![6, 5, 4, 3, 2, 1];
        counting_sort(&mut ve1, 6);

        assert!(is_sorted(&ve1));
    }

    #[test]
    fn counting_sort_pre_sorted() {
        let mut ve2 = vec![1, 2, 3, 4, 5, 6];
        counting_sort(&mut ve2, 6);

        assert!(is_sorted(&ve2));
    }

    #[test]
    fn generic_counting_sort() {
        let mut ve1: Vec<u8> = vec![100, 30, 60, 10, 20, 120, 1];
        super::generic_counting_sort(&mut ve1, 120);

        assert!(is_sorted(&ve1));
    }

    #[test]
    fn presorted_u64_counting_sort() {
        let mut ve2: Vec<u64> = vec![1, 2, 3, 4, 5, 6];
        super::generic_counting_sort(&mut ve2, 6);

        assert!(is_sorted(&ve2));
    }
}
}

地精排序

#![allow(unused)]
fn main() {
use std::cmp;

pub fn gnome_sort<T>(arr: &[T]) -> Vec<T>
where
    T: cmp::PartialEq + cmp::PartialOrd + Clone,
{
    let mut arr = arr.to_vec();
    let mut i: usize = 1;
    let mut j: usize = 2;

    while i < arr.len() {
        if arr[i - 1] < arr[i] {
            i = j;
            j = i + 1;
        } else {
            arr.swap(i - 1, i);
            i -= 1;
            if i == 0 {
                i = j;
                j += 1;
            }
        }
    }
    arr
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        let res = gnome_sort(&vec![6, 5, -8, 3, 2, 3]);
        assert_eq!(res, vec![-8, 2, 3, 3, 5, 6]);
    }

    #[test]
    fn already_sorted() {
        let res = gnome_sort(&vec!["a", "b", "c"]);
        assert_eq!(res, vec!["a", "b", "c"]);
    }

    #[test]
    fn odd_number_of_elements() {
        let res = gnome_sort(&vec!["d", "a", "c", "e", "b"]);
        assert_eq!(res, vec!["a", "b", "c", "d", "e"]);
    }

    #[test]
    fn one_element() {
        let res = gnome_sort(&vec![3]);
        assert_eq!(res, vec![3]);
    }

    #[test]
    fn empty() {
        let res = gnome_sort(&Vec::<u8>::new());
        assert_eq!(res, vec![]);
    }
}
}

堆排序

#![allow(unused)]
fn main() {
pub fn heap_sort<T: PartialOrd>(arr: &mut [T]) {
    let size = arr.len();
    // 构建大根堆
    for i in (0..size / 2).rev() {
        heapify(arr, i, size);
    }

    // 每轮循环将堆顶元素（也就是最大元素）放到最后
    for i in (1..size).rev() {
        arr.swap(0, i);
        // 恢复大根堆
        heapify(arr, 0, i);
    }
}

fn heapify<T: PartialOrd>(arr: &mut [T], root: usize, end: usize) {
    // 记录父节点和左右节点中最大元素的索引位置
    let mut largest = root;

    let left_child = 2 * root + 1;
    if left_child < end && arr[left_child] > arr[largest] {
        largest = left_child;
    }

    let right_child = left_child + 1;
    if right_child < end && arr[right_child] > arr[largest] {
        largest = right_child;
    }

    if largest != root {
        arr.swap(root, largest);
        heapify(arr, largest, end);
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_empty_vec() {
        let mut empty_vec: Vec<String> = vec![];
        heap_sort(&mut empty_vec);
        assert_eq!(empty_vec, Vec::<String>::new());
    }

    #[test]
    fn test_number_vec() {
        let mut vec = vec![7, 49, 73, 58, 30, 72, 44, 78, 23, 9];
        heap_sort(&mut vec);
        assert_eq!(vec, vec![7, 9, 23, 30, 44, 49, 58, 72, 73, 78]);
    }

    #[test]
    fn test_string_vec() {
        let mut vec = vec![
            String::from("Bob"),
            String::from("David"),
            String::from("Carol"),
            String::from("Alice"),
        ];
        heap_sort(&mut vec);
        assert_eq!(
            vec,
            vec![
                String::from("Alice"),
                String::from("Bob"),
                String::from("Carol"),
                String::from("David"),
            ]
        );
    }
}
}

插入排序

#![allow(unused)]
fn main() {
pub fn insertion_sort<T: PartialOrd>(arr: &mut [T]) {
    // 从第二个元素开始排序
    for i in 1..arr.len() {
        // 找到 arr[i] 该插入的位置
        let mut j = i;
        while j > 0 && arr[j - 1] > arr[j] {
            arr.swap(j - 1, j);
            j -= 1;
        }
    }
}

// 这里需要 T: Ord 是因为 binary_search() 方法的限制
pub fn insertion_sort_binary_search<T: Ord>(arr: &mut[T]) {
    // 从第二个元素开始排序
    for i in 1..arr.len() {
        // 利用二分查找获取 arr[i] 应该插入的位置
        let pos = arr[..i].binary_search(&arr[i]).unwrap_or_else(|pos| pos);
        let mut j = i;
        while j > pos {
            arr.swap(j - 1, j);
            j -= 1;
        }
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    mod insertion_sort {
        use super::*;

        #[test]
        fn test_empty_vec() {
            let mut empty_vec: Vec<String> = vec![];
            insertion_sort(&mut empty_vec);
            assert_eq!(empty_vec, Vec::<String>::new());
        }
    
        #[test]
        fn test_number_vec() {
            let mut vec = vec![7, 49, 73, 58, 30, 72, 44, 78, 23, 9];
            insertion_sort(&mut vec);
            assert_eq!(vec, vec![7, 9, 23, 30, 44, 49, 58, 72, 73, 78]);
        }
    
        #[test]
        fn test_string_vec() {
            let mut vec = vec![
                String::from("Bob"),
                String::from("David"),
                String::from("Carol"),
                String::from("Alice"),
            ];
            insertion_sort(&mut vec);
            assert_eq!(
                vec,
                vec![
                    String::from("Alice"),
                    String::from("Bob"),
                    String::from("Carol"),
                    String::from("David"),
                ]
            );
        }
    }

    mod insertion_sort_binary_search {
        use super::*;
        
        #[test]
        fn test_empty_vec() {
            let mut empty_vec: Vec<String> = vec![];
            insertion_sort_binary_search(&mut empty_vec);
            assert_eq!(empty_vec, Vec::<String>::new());
        }
    
        #[test]
        fn test_number_vec() {
            let mut vec = vec![7, 49, 73, 58, 30, 72, 44, 78, 23, 9];
            insertion_sort_binary_search(&mut vec);
            assert_eq!(vec, vec![7, 9, 23, 30, 44, 49, 58, 72, 73, 78]);
        }
    
        #[test]
        fn test_string_vec() {
            let mut vec = vec![
                String::from("Bob"),
                String::from("David"),
                String::from("Carol"),
                String::from("Alice"),
            ];
            insertion_sort_binary_search(&mut vec);
            assert_eq!(
                vec,
                vec![
                    String::from("Alice"),
                    String::from("Bob"),
                    String::from("Carol"),
                    String::from("David"),
                ]
            );
        }
    }
}
}

归并排序

#![allow(unused)]
fn main() {
pub fn merge_sort<T>(arr: &mut [T])
where
    T: PartialOrd + Clone + Default,
{
    if arr.len() > 1 {
        merge_sort_range(arr, 0, arr.len() - 1);
    }
}

fn merge_sort_range<T>(arr: &mut [T], lo: usize, hi: usize)
where
    T: PartialOrd + Clone + Default,
{
    // 只有当元素个数大于一时才进行排序
    if lo < hi {
        let mid = lo + ((hi - lo) >> 1);
        merge_sort_range(arr, lo, mid);
        merge_sort_range(arr, mid + 1, hi);
        merge_two_arrays(arr, lo, mid, hi);
    }
}

// 合并两个有序数组: arr[lo..=mid], arr[mid + 1..=hi]
fn merge_two_arrays<T>(arr: &mut [T], lo: usize, mid: usize, hi: usize)
where
    T: PartialOrd + Clone + Default,
{
    // 这里需要 clone 数组元素
    let mut arr1 = arr[lo..=mid].to_vec();
    let mut arr2 = arr[mid + 1..=hi].to_vec();

    let (mut i, mut j) = (0, 0);
    while i < arr1.len() && j < arr2.len() {
        if arr1[i] < arr2[j] {
            arr[i + j + lo] = std::mem::take(&mut arr1[i]);
            i += 1;
        } else {
            arr[i + j + lo] = std::mem::take(&mut arr2[j]);
            j += 1;
        }
    }

    while i < arr1.len() {
        arr[i + j + lo] = std::mem::take(&mut arr1[i]);
        i += 1;
    }

    while j < arr2.len() {
        arr[i + j + lo] = std::mem::take(&mut arr2[j]);
        j += 1;
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_empty_vec() {
        let mut empty_vec: Vec<String> = vec![];
        merge_sort(&mut empty_vec);
        assert_eq!(empty_vec, Vec::<String>::new());
    }

    #[test]
    fn test_number_vec() {
        let mut vec = vec![7, 49, 73, 58, 30, 72, 44, 78, 23, 9];
        merge_sort(&mut vec);
        assert_eq!(vec, vec![7, 9, 23, 30, 44, 49, 58, 72, 73, 78]);
    }

    #[test]
    fn test_string_vec() {
        let mut vec = vec![
            String::from("Bob"),
            String::from("David"),
            String::from("Carol"),
            String::from("Alice"),
        ];
        merge_sort(&mut vec);
        assert_eq!(
            vec,
            vec![
                String::from("Alice"),
                String::from("Bob"),
                String::from("Carol"),
                String::from("David"),
            ]
        );
    }
}
}

奇偶排序

#![allow(unused)]
fn main() {
pub fn odd_even_sort<T: Ord>(arr: &mut [T]) {
    let len = arr.len();
    if len == 0 {
        return;
    }

    let mut sorted = false;
    while !sorted {
        sorted = true;

        for i in (1..len - 1).step_by(2) {
            if arr[i] > arr[i + 1] {
                arr.swap(i, i + 1);
                sorted = false;
            }
        }

        for i in (0..len - 1).step_by(2) {
            if arr[i] > arr[i + 1] {
                arr.swap(i, i + 1);
                sorted = false;
            }
        }
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        let mut arr = vec![3, 5, 1, 2, 4, 6];
        odd_even_sort(&mut arr);
        assert_eq!(arr, vec![1, 2, 3, 4, 5, 6]);
    }

    #[test]
    fn empty() {
        let mut arr = Vec::<i32>::new();
        odd_even_sort(&mut arr);
        assert_eq!(arr, vec![]);
    }

    #[test]
    fn one_element() {
        let mut arr = vec![3];
        odd_even_sort(&mut arr);
        assert_eq!(arr, vec![3]);
    }

    #[test]
    fn pre_sorted() {
        let mut arr = vec![0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
        odd_even_sort(&mut arr);
        assert_eq!(arr, vec![0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
    }
}
}

快速排序

#![allow(unused)]
fn main() {
pub fn quick_sort<T: PartialOrd>(arr: &mut [T]) {
    if arr.len() > 1 {
        quick_sort_range(arr, 0, arr.len() - 1);
    }
}

fn quick_sort_range<T: PartialOrd>(arr: &mut [T], lo: usize, hi: usize) {
    // 只有当元素个数大于一时才进行排序
    if lo < hi {
        let pos = partition(arr, lo, hi);
        // let pos = partition_random(arr, lo, hi);
        if pos != 0 {
            // 如果 pos == 0, pos - 1 会发生溢出错误
            quick_sort_range(arr, lo, pos - 1);
        }
        quick_sort_range(arr, pos + 1, hi);
    }
}

fn partition<T: PartialOrd>(arr: &mut [T], lo: usize, hi: usize) -> usize {
    // 默认选取 lo 作为 pivot
    let pivot = lo;

    let (mut left, mut right) = (lo, hi);
    while left < right {
        // 找到右边第一个不大于等于 arr[pivot] 的元素
        while left < right && arr[right] >= arr[pivot] {
            right -= 1;
        }

        // 找到左边第一个不小于等于 arr[pivot] 的元素
        while left < right && arr[left] <= arr[pivot] {
            left += 1;
        }
        
        // 交换前面找到的两个元素
        if left != right {
            arr.swap(left, right);
        }
    }

    arr.swap(pivot, left);

    // 返回正确的分割位置
    left
}

// 随机选取 pivot 的位置
fn partition_random<T: PartialOrd>(arr: &mut [T], lo: usize, hi: usize) -> usize {
    // 在 Cargo.toml 的依赖中添加 rand 库
    use rand::Rng;
    let mut rng = rand::thread_rng();
    let pivot = rng.gen_range(lo..=hi);

    // 交换 lo 和 pivot 位置上的元素，从而间接使得 pivot = lo
    // 因此后序操作和 partition() 函数一致
    arr.swap(lo, pivot);

    let pivot = lo;
    let (mut left, mut right) = (lo, hi);
    while left < right {
        // 找到右边第一个不大于等于 arr[pivot] 的元素
        while left < right && arr[right] >= arr[pivot] {
            right -= 1;
        }

        // 找到左边第一个不小于等于 arr[pivot] 的元素
        while left < right && arr[left] <= arr[pivot] {
            left += 1;
        }
        
        // 交换前面找到的两个元素
        if left != right {
            arr.swap(left, right);
        }
    }

    arr.swap(pivot, left);

    // 返回正确的分割位置
    left
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_empty_vec() {
        let mut empty_vec: Vec<String> = vec![];
        quick_sort(&mut empty_vec);
        assert_eq!(empty_vec, Vec::<String>::new());
    }

    #[test]
    fn test_number_vec() {
        let mut vec = vec![7, 49, 73, 58, 30, 72, 44, 78, 23, 9];
        quick_sort(&mut vec);
        assert_eq!(vec, vec![7, 9, 23, 30, 44, 49, 58, 72, 73, 78]);
    }

    #[test]
    fn test_string_vec() {
        let mut vec = vec![
            String::from("Bob"),
            String::from("David"),
            String::from("Carol"),
            String::from("Alice"),
        ];
        quick_sort(&mut vec);
        assert_eq!(
            vec,
            vec![
                String::from("Alice"),
                String::from("Bob"),
                String::from("Carol"),
                String::from("David"),
            ]
        );
    }
}
}

基数排序

#![allow(unused)]
fn main() {
/// Sorts the elements of `arr` in-place using radix sort.
///
/// Time complexity is `O((n + b) * logb(k))`, where `n` is the number of elements,
/// `b` is the base (the radix), and `k` is the largest element.
/// When `n` and `b` are roughly the same maginitude, this algorithm runs in linear time.
///
/// Space complexity is `O(n + b)`.
pub fn radix_sort(arr: &mut [u64]) {
    let max: usize = match arr.iter().max() {
        Some(&x) => x as usize,
        None => return,
    };
    // Make radix a power of 2 close to arr.len() for optimal runtime
    let radix = arr.len().next_power_of_two();
    // Counting sort by each digit from least to most significant
    let mut place = 1;
    while place <= max {
        let digit_of = |x| x as usize / place % radix;
        // Count digit occurrences
        let mut counter = vec![0; radix];
        for &x in arr.iter() {
            counter[digit_of(x)] += 1;
        }
        // Compute last index of each digit
        for i in 1..radix {
            counter[i] += counter[i - 1];
        }
        // Write elements to their new indices
        for &x in arr.to_owned().iter().rev() {
            counter[digit_of(x)] -= 1;
            arr[counter[digit_of(x)]] = x;
        }
        place *= radix;
    }
}

#[cfg(test)]
mod tests {
    use super::super::is_sorted;
    use super::radix_sort;

    #[test]
    fn empty() {
        let mut a: [u64; 0] = [];
        radix_sort(&mut a);
        assert!(is_sorted(&a));
    }

    #[test]
    fn descending() {
        let mut v = vec![201, 127, 64, 37, 24, 4, 1];
        radix_sort(&mut v);
        assert!(is_sorted(&v));
    }

    #[test]
    fn ascending() {
        let mut v = vec![1, 4, 24, 37, 64, 127, 201];
        radix_sort(&mut v);
        assert!(is_sorted(&v));
    }
}
}

选择排序

#![allow(unused)]
fn main() {
pub fn selection_sort<T: PartialOrd>(arr: &mut [T]) {
    if arr.len() <= 1 {
        return;
    }

    let size = arr.len();
    for i in 0..(size - 1) {
        // 找到最小元素的索引值
        let mut min_index = i;
        for j in (i + 1)..size {
            if arr[j] < arr[min_index] {
                min_index = j;
            }
        }

        if min_index != i {
            arr.swap(i, min_index);
        }
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_empty_vec() {
        let mut empty_vec: Vec<String> = vec![];
        selection_sort(&mut empty_vec);
        assert_eq!(empty_vec, Vec::<String>::new());
    }

    #[test]
    fn test_number_vec() {
        let mut vec = vec![7, 49, 73, 58, 30, 72, 44, 78, 23, 9];
        selection_sort(&mut vec);
        assert_eq!(vec, vec![7, 9, 23, 30, 44, 49, 58, 72, 73, 78]);
    }

    #[test]
    fn test_string_vec() {
        let mut vec = vec![
            String::from("Bob"),
            String::from("David"),
            String::from("Carol"),
            String::from("Alice"),
        ];
        selection_sort(&mut vec);
        assert_eq!(
            vec,
            vec![
                String::from("Alice"),
                String::from("Bob"),
                String::from("Carol"),
                String::from("David"),
            ]
        );
    }
}
}

希尔排序

#![allow(unused)]
fn main() {
pub fn shell_sort<T: Ord + Copy>(values: &mut Vec<T>) {
    // shell sort works by swiping the value at a given gap and decreasing the gap to 1
    fn insertion<T: Ord + Copy>(values: &mut Vec<T>, start: usize, gap: usize) {
        for i in ((start + gap)..values.len()).step_by(gap) {
            let val_current = values[i];
            let mut pos = i;
            // make swaps
            while pos >= gap && values[pos - gap] > val_current {
                values[pos] = values[pos - gap];
                pos -= gap;
            }
            values[pos] = val_current;
        }
    }

    let mut count_sublist = values.len() / 2; // makes gap as long as half of the array
    while count_sublist > 0 {
        for pos_start in 0..count_sublist {
            insertion(values, pos_start, count_sublist);
        }
        count_sublist /= 2; // makes gap as half of previous
    }
}

#[cfg(test)]
mod test {
    use super::shell_sort;

    #[test]
    fn basic() {
        let mut vec = vec![3, 5, 6, 3, 1, 4];
        shell_sort(&mut vec);
        for i in 0..vec.len() - 1 {
            assert!(vec[i] <= vec[i + 1]);
        }
    }

    #[test]
    fn empty() {
        let mut vec: Vec<i32> = vec![];
        shell_sort(&mut vec);
        assert_eq!(vec, vec![]);
    }

    #[test]
    fn reverse() {
        let mut vec = vec![6, 5, 4, 3, 2, 1];
        shell_sort(&mut vec);
        for i in 0..vec.len() - 1 {
            assert!(vec[i] <= vec[i + 1]);
        }
    }

    #[test]
    fn already_sorted() {
        let mut vec = vec![1, 2, 3, 4, 5, 6];
        shell_sort(&mut vec);
        for i in 0..vec.len() - 1 {
            assert!(vec[i] <= vec[i + 1]);
        }
    }
}
}

臭皮匠排序

#![allow(unused)]
fn main() {
fn _stooge_sort<T: Ord>(arr: &mut [T], start: usize, end: usize) {
    if arr[start] > arr[end] {
        arr.swap(start, end);
    }

    if start + 1 >= end {
        return;
    }

    let k = (end - start + 1) / 3;

    _stooge_sort(arr, start, end - k);
    _stooge_sort(arr, start + k, end);
    _stooge_sort(arr, start, end - k);
}

pub fn stooge_sort<T: Ord>(arr: &mut [T]) {
    let len = arr.len();
    if len == 0 {
        return;
    }

    _stooge_sort(arr, 0, len - 1);
}

#[cfg(test)]
mod test {
    use super::*;

    #[test]
    fn basic() {
        let mut vec = vec![3, 5, 6, 3, 1, 4];
        stooge_sort(&mut vec);
        for i in 0..vec.len() - 1 {
            assert!(vec[i] <= vec[i + 1]);
        }
    }

    #[test]
    fn empty() {
        let mut vec: Vec<i32> = vec![];
        stooge_sort(&mut vec);
        assert_eq!(vec, vec![]);
    }

    #[test]
    fn reverse() {
        let mut vec = vec![6, 5, 4, 3, 2, 1];
        stooge_sort(&mut vec);
        for i in 0..vec.len() - 1 {
            assert!(vec[i] <= vec[i + 1]);
        }
    }

    #[test]
    fn already_sorted() {
        let mut vec = vec![1, 2, 3, 4, 5, 6];
        stooge_sort(&mut vec);
        for i in 0..vec.len() - 1 {
            assert!(vec[i] <= vec[i + 1]);
        }
    }
}
}

字符串

字符串相关的算法往往和子串匹配、顺序调整相关，如何高效的处理字符串，有时会成为一个程序性能的关键。

逆序倒转

#![allow(unused)]
fn main() {
pub fn reverse(text: &str) -> String {
    text.chars().rev().collect()
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_simple() {
        assert_eq!(reverse("racecar"), "racecar");
    }

    #[test]
    fn test_sentence() {
        assert_eq!(reverse("step on no pets"), "step on no pets");
    }
}
}

数据转换算法(Burrows Wheeler Transform)

#![allow(unused)]
fn main() {
pub fn burrows_wheeler_transform(input: String) -> (String, usize) {
    let len = input.len();

    let mut table = Vec::<String>::with_capacity(len);
    for i in 0..len {
        table.push(input[i..].to_owned() + &input[..i]);
    }
    table.sort_by_key(|a| a.to_lowercase());

    let mut encoded = String::new();
    let mut index: usize = 0;
    for (i, item) in table.iter().enumerate().take(len) {
        encoded.push(item.chars().last().unwrap());
        if item.eq(&input) {
            index = i;
        }
    }

    (encoded, index)
}

pub fn inv_burrows_wheeler_transform(input: (String, usize)) -> String {
    let len = input.0.len();
    let mut table = Vec::<(usize, char)>::with_capacity(len);
    for i in 0..len {
        table.push((i, input.0.chars().nth(i).unwrap()));
    }

    table.sort_by(|a, b| a.1.cmp(&b.1));

    let mut decoded = String::new();
    let mut idx = input.1;
    for _ in 0..len {
        decoded.push(table[idx].1);
        idx = table[idx].0;
    }

    decoded
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform("CARROT".to_string())),
            "CARROT"
        );
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform("TOMATO".to_string())),
            "TOMATO"
        );
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform("THISISATEST".to_string())),
            "THISISATEST"
        );
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform("THEALGORITHMS".to_string())),
            "THEALGORITHMS"
        );
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform("RUST".to_string())),
            "RUST"
        );
    }

    #[test]
    fn special_characters() {
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform("!.!.!??.=::".to_string())),
            "!.!.!??.=::"
        );
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform(
                "!{}{}(((&&%%!??.=::".to_string()
            )),
            "!{}{}(((&&%%!??.=::"
        );
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform("//&$[]".to_string())),
            "//&$[]"
        );
    }

    #[test]
    fn empty() {
        assert_eq!(
            inv_burrows_wheeler_transform(burrows_wheeler_transform("".to_string())),
            ""
        );
    }
}
}

KMP算法(Knuth Morris Pratt)

#![allow(unused)]
fn main() {
pub fn knuth_morris_pratt(st: String, pat: String) -> Vec<usize> {
    if st.is_empty() || pat.is_empty() {
        return vec![];
    }

    let string = st.into_bytes();
    let pattern = pat.into_bytes();

    // build the partial match table
    let mut partial = vec![0];
    for i in 1..pattern.len() {
        let mut j = partial[i - 1];
        while j > 0 && pattern[j] != pattern[i] {
            j = partial[j - 1];
        }
        partial.push(if pattern[j] == pattern[i] { j + 1 } else { j });
    }

    // and read 'string' to find 'pattern'
    let mut ret = vec![];
    let mut j = 0;

    for (i, &c) in string.iter().enumerate() {
        while j > 0 && c != pattern[j] {
            j = partial[j - 1];
        }
        if c == pattern[j] {
            j += 1;
        }
        if j == pattern.len() {
            ret.push(i + 1 - j);
            j = partial[j - 1];
        }
    }

    ret
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn each_letter_matches() {
        let index = knuth_morris_pratt("aaa".to_string(), "a".to_string());
        assert_eq!(index, vec![0, 1, 2]);
    }

    #[test]
    fn a_few_separate_matches() {
        let index = knuth_morris_pratt("abababa".to_string(), "ab".to_string());
        assert_eq!(index, vec![0, 2, 4]);
    }

    #[test]
    fn one_match() {
        let index =
            knuth_morris_pratt("ABC ABCDAB ABCDABCDABDE".to_string(), "ABCDABD".to_string());
        assert_eq!(index, vec![15]);
    }

    #[test]
    fn lots_of_matches() {
        let index = knuth_morris_pratt("aaabaabaaaaa".to_string(), "aa".to_string());
        assert_eq!(index, vec![0, 1, 4, 7, 8, 9, 10]);
    }

    #[test]
    fn lots_of_intricate_matches() {
        let index = knuth_morris_pratt("ababababa".to_string(), "aba".to_string());
        assert_eq!(index, vec![0, 2, 4, 6]);
    }

    #[test]
    fn not_found0() {
        let index = knuth_morris_pratt("abcde".to_string(), "f".to_string());
        assert_eq!(index, vec![]);
    }

    #[test]
    fn not_found1() {
        let index = knuth_morris_pratt("abcde".to_string(), "ac".to_string());
        assert_eq!(index, vec![]);
    }

    #[test]
    fn not_found2() {
        let index = knuth_morris_pratt("ababab".to_string(), "bababa".to_string());
        assert_eq!(index, vec![]);
    }

    #[test]
    fn empty_string() {
        let index = knuth_morris_pratt("".to_string(), "abcdef".to_string());
        assert_eq!(index, vec![]);
    }
}
}

马拉车算法(Manacher)

#![allow(unused)]
fn main() {
pub fn manacher(s: String) -> String {
    let l = s.len();
    if l <= 1 {
        return s;
    }

    // MEMO: We need to detect odd palindrome as well,
    // therefore, inserting dummy string so that
    // we can find a pair with dummy center character.
    let mut chars: Vec<char> = Vec::with_capacity(s.len() * 2 + 1);
    for c in s.chars() {
        chars.push('#');
        chars.push(c);
    }
    chars.push('#');

    // List: storing the length of palindrome at each index of string
    let mut length_of_palindrome = vec![1usize; chars.len()];
    // Integer: Current checking palindrome's center index
    let mut current_center: usize = 0;
    // Integer: Right edge index existing the radius away from current center
    let mut right_from_current_center: usize = 0;

    for i in 0..chars.len() {
        // 1: Check if we are looking at right side of palindrome.
        if right_from_current_center > i && i > current_center {
            // 1-1: If so copy from the left side of palindrome.
            // If the value + index exceeds the right edge index, we should cut and check palindrome later #3.
            length_of_palindrome[i] = std::cmp::min(
                right_from_current_center - i,
                length_of_palindrome[2 * current_center - i],
            );
            // 1-2: Move the checking palindrome to new index if it exceeds the right edge.
            if length_of_palindrome[i] + i >= right_from_current_center {
                current_center = i;
                right_from_current_center = length_of_palindrome[i] + i;
                // 1-3: If radius exceeds the end of list, it means checking is over.
                // You will never get the larger value because the string will get only shorter.
                if right_from_current_center >= chars.len() - 1 {
                    break;
                }
            } else {
                // 1-4: If the checking index doesn't exceeds the right edge,
                // it means the length is just as same as the left side.
                // You don't need to check anymore.
                continue;
            }
        }

        // Integer: Current radius from checking index
        // If it's copied from left side and more than 1,
        // it means it's ensured so you don't need to check inside radius.
        let mut radius: usize = (length_of_palindrome[i] - 1) / 2;
        radius += 1;
        // 2: Checking palindrome.
        // Need to care about overflow usize.
        while i >= radius && i + radius <= chars.len() - 1 && chars[i - radius] == chars[i + radius]
        {
            length_of_palindrome[i] += 2;
            radius += 1;
        }
    }

    // 3: Find the maximum length and generate answer.
    let center_of_max = length_of_palindrome
        .iter()
        .enumerate()
        .max_by_key(|(_, &value)| value)
        .map(|(idx, _)| idx)
        .unwrap();
    let radius_of_max = (length_of_palindrome[center_of_max] - 1) / 2;
    let answer = &chars[(center_of_max - radius_of_max)..(center_of_max + radius_of_max + 1)]
        .iter()
        .collect::<String>();
    answer.replace("#", "")
}

#[cfg(test)]
mod tests {
    use super::manacher;

    #[test]
    fn get_longest_palindrome_by_manacher() {
        assert_eq!(manacher("babad".to_string()), "aba".to_string());
        assert_eq!(manacher("cbbd".to_string()), "bb".to_string());
        assert_eq!(manacher("a".to_string()), "a".to_string());

        let ac_ans = manacher("ac".to_string());
        assert!(ac_ans == "a".to_string() || ac_ans == "c".to_string());
    }
}
}

Rabin Karp算法

#![allow(unused)]
fn main() {
pub fn rabin_karp(target: String, pattern: String) -> Vec<usize> {
    // Quick exit
    if target.is_empty() || pattern.is_empty() || pattern.len() > target.len() {
        return vec![];
    }

    let string: String = (&pattern[0..pattern.len()]).to_string();
    let hash_pattern = hash(string.clone());
    let mut ret = vec![];
    for i in 0..(target.len() - pattern.len() + 1) {
        let s = (&target[i..(i + pattern.len())]).to_string();
        let string_hash = hash(s.clone());

        if string_hash == hash_pattern && s == string {
            ret.push(i);
        }
    }
    ret
}

fn hash(mut s: String) -> u16 {
    let prime: u16 = 101;
    let last_char = s
        .drain(s.len() - 1..)
        .next()
        .expect("Failed to get the last char of the string");
    let mut res: u16 = 0;
    for (i, &c) in s.as_bytes().iter().enumerate() {
        if i == 0 {
            res = (c as u16 * 256) % prime;
        } else {
            res = (((res + c as u16) % 101) * 256) % 101;
        }
    }
    (res + last_char as u16) % prime
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn hi_hash() {
        let hash_result = hash("hi".to_string());
        assert_eq!(hash_result, 65);
    }

    #[test]
    fn abr_hash() {
        let hash_result = hash("abr".to_string());
        assert_eq!(hash_result, 4);
    }

    #[test]
    fn bra_hash() {
        let hash_result = hash("bra".to_string());
        assert_eq!(hash_result, 30);
    }

    // Attribution to @pgimalac for his tests from Knuth-Morris-Pratt
    #[test]
    fn each_letter_matches() {
        let index = rabin_karp("aaa".to_string(), "a".to_string());
        assert_eq!(index, vec![0, 1, 2]);
    }

    #[test]
    fn a_few_separate_matches() {
        let index = rabin_karp("abababa".to_string(), "ab".to_string());
        assert_eq!(index, vec![0, 2, 4]);
    }

    #[test]
    fn one_match() {
        let index = rabin_karp("ABC ABCDAB ABCDABCDABDE".to_string(), "ABCDABD".to_string());
        assert_eq!(index, vec![15]);
    }

    #[test]
    fn lots_of_matches() {
        let index = rabin_karp("aaabaabaaaaa".to_string(), "aa".to_string());
        assert_eq!(index, vec![0, 1, 4, 7, 8, 9, 10]);
    }

    #[test]
    fn lots_of_intricate_matches() {
        let index = rabin_karp("ababababa".to_string(), "aba".to_string());
        assert_eq!(index, vec![0, 2, 4, 6]);
    }

    #[test]
    fn not_found0() {
        let index = rabin_karp("abcde".to_string(), "f".to_string());
        assert_eq!(index, vec![]);
    }

    #[test]
    fn not_found1() {
        let index = rabin_karp("abcde".to_string(), "ac".to_string());
        assert_eq!(index, vec![]);
    }

    #[test]
    fn not_found2() {
        let index = rabin_karp("ababab".to_string(), "bababa".to_string());
        assert_eq!(index, vec![]);
    }

    #[test]
    fn empty_string() {
        let index = rabin_karp("".to_string(), "abcdef".to_string());
        assert_eq!(index, vec![]);
    }
}
}

查找算法

查找是在大量的信息中寻找一个特定的信息元素，在计算机应用中，查找是常用的基本运算，例如编译程序中符号表的查找。

把数据按照合适的方式进行排列，往往是查找的关键。

二分搜索

From Wikipedia: Binary search, also known as half-interval search or logarithmic search, is a search algorithm that finds the position of a target value within a sorted array. It compares the target value to the middle element of the array; if they are unequal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful.

Properties

• Worst case performance O(log n)
• Best case performance O(1)
• Average case performance O(log n)
• Worst case space complexity O(1)

#![allow(unused)]
fn main() {
use std::cmp::Ordering;

pub fn binary_search<T: Ord>(item: &T, arr: &[T]) -> Option<usize> {
    let mut left = 0;
    let mut right = arr.len();

    while left < right {
        let mid = left + (right - left) / 2;

        match item.cmp(&arr[mid]) {
            Ordering::Less => right = mid,
            Ordering::Equal => return Some(mid),
            Ordering::Greater => left = mid + 1,
        }
    }
    None
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn empty() {
        let index = binary_search(&"a", &vec![]);
        assert_eq!(index, None);
    }

    #[test]
    fn one_item() {
        let index = binary_search(&"a", &vec!["a"]);
        assert_eq!(index, Some(0));
    }

    #[test]
    fn search_strings() {
        let index = binary_search(&"a", &vec!["a", "b", "c", "d", "google", "zoo"]);
        assert_eq!(index, Some(0));
    }

    #[test]
    fn search_ints() {
        let index = binary_search(&4, &vec![1, 2, 3, 4]);
        assert_eq!(index, Some(3));

        let index = binary_search(&3, &vec![1, 2, 3, 4]);
        assert_eq!(index, Some(2));

        let index = binary_search(&2, &vec![1, 2, 3, 4]);
        assert_eq!(index, Some(1));

        let index = binary_search(&1, &vec![1, 2, 3, 4]);
        assert_eq!(index, Some(0));
    }

    #[test]
    fn not_found() {
        let index = binary_search(&5, &vec![1, 2, 3, 4]);
        assert_eq!(index, None);
    }
}
}

递归二分查找

#![allow(unused)]
fn main() {
use std::cmp::Ordering;

pub fn binary_search_rec<T: Ord>(
    list_of_items: &[T],
    target: &T,
    left: &usize,
    right: &usize,
) -> Option<usize> {
    if left >= right {
        return None;
    }

    let middle: usize = left + (right - left) / 2;
    match target.cmp(&list_of_items[middle]) {
        Ordering::Less => binary_search_rec(list_of_items, target, left, &middle),
        Ordering::Greater => binary_search_rec(list_of_items, target, &(middle + 1), right),
        Ordering::Equal => Some(middle),
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    const LEFT: usize = 0;

    #[test]
    fn fail_empty_list() {
        let list_of_items = vec![];
        assert_eq!(
            binary_search_rec(&list_of_items, &1, &LEFT, &list_of_items.len()),
            None
        );
    }

    #[test]
    fn success_one_item() {
        let list_of_items = vec![30];
        assert_eq!(
            binary_search_rec(&list_of_items, &30, &LEFT, &list_of_items.len()),
            Some(0)
        );
    }

    #[test]
    fn success_search_strings() {
        let say_hello_list = vec!["hi", "olá", "salut"];
        let right = say_hello_list.len();
        assert_eq!(
            binary_search_rec(&say_hello_list, &"hi", &LEFT, &right),
            Some(0)
        );
        assert_eq!(
            binary_search_rec(&say_hello_list, &"salut", &LEFT, &right),
            Some(2)
        );
    }

    #[test]
    fn fail_search_strings() {
        let say_hello_list = vec!["hi", "olá", "salut"];
        for target in &["adiós", "你好"] {
            assert_eq!(
                binary_search_rec(&say_hello_list, target, &LEFT, &say_hello_list.len()),
                None
            );
        }
    }

    #[test]
    fn success_search_integers() {
        let integers = vec![0, 10, 20, 30, 40, 50, 60, 70, 80, 90];
        for (index, target) in integers.iter().enumerate() {
            assert_eq!(
                binary_search_rec(&integers, target, &LEFT, &integers.len()),
                Some(index)
            )
        }
    }

    #[test]
    fn fail_search_integers() {
        let integers = vec![0, 10, 20, 30, 40, 50, 60, 70, 80, 90];
        for target in &[100, 444, 336] {
            assert_eq!(
                binary_search_rec(&integers, target, &LEFT, &integers.len()),
                None
            );
        }
    }

    #[test]
    fn fail_search_unsorted_strings_list() {
        let unsorted_strings = vec!["salut", "olá", "hi"];
        for target in &["hi", "salut"] {
            assert_eq!(
                binary_search_rec(&unsorted_strings, target, &LEFT, &unsorted_strings.len()),
                None
            );
        }
    }

    #[test]
    fn fail_search_unsorted_integers_list() {
        let unsorted_integers = vec![90, 80, 70, 60, 50, 40, 30, 20, 10, 0];
        for target in &[0, 80, 90] {
            assert_eq!(
                binary_search_rec(&unsorted_integers, target, &LEFT, &unsorted_integers.len()),
                None
            );
        }
    }

    #[test]
    fn success_search_string_in_middle_of_unsorted_list() {
        let unsorted_strings = vec!["salut", "olá", "hi"];
        assert_eq!(
            binary_search_rec(&unsorted_strings, &"olá", &LEFT, &unsorted_strings.len()),
            Some(1)
        );
    }

    #[test]
    fn success_search_integer_in_middle_of_unsorted_list() {
        let unsorted_integers = vec![90, 80, 70];
        assert_eq!(
            binary_search_rec(&unsorted_integers, &80, &LEFT, &unsorted_integers.len()),
            Some(1)
        );
    }
}
}

查找第K小的元素

#![allow(unused)]
fn main() {
use crate::sorting::partition;
use std::cmp::{Ordering, PartialOrd};

/// Returns k-th smallest element of an array, i.e. its order statistics.
/// Time complexity is O(n^2) in the worst case, but only O(n) on average.
/// It mutates the input, and therefore does not require additional space.
pub fn kth_smallest<T>(input: &mut [T], k: usize) -> Option<T>
where
    T: PartialOrd + Copy,
{
    if input.is_empty() {
        return None;
    }

    let kth = _kth_smallest(input, k, 0, input.len() - 1);
    Some(kth)
}

fn _kth_smallest<T>(input: &mut [T], k: usize, lo: usize, hi: usize) -> T
where
    T: PartialOrd + Copy,
{
    if lo == hi {
        return input[lo];
    }

    let pivot = partition(input, lo as isize, hi as isize) as usize;
    let i = pivot - lo + 1;

    match k.cmp(&i) {
        Ordering::Equal => input[pivot],
        Ordering::Less => _kth_smallest(input, k, lo, pivot - 1),
        Ordering::Greater => _kth_smallest(input, k - i, pivot + 1, hi),
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn empty() {
        let mut zero: [u8; 0] = [];
        let first = kth_smallest(&mut zero, 1);

        assert_eq!(None, first);
    }

    #[test]
    fn one_element() {
        let mut one = [1];
        let first = kth_smallest(&mut one, 1);

        assert_eq!(1, first.unwrap());
    }

    #[test]
    fn many_elements() {
        // 0 1 3 4 5 7 8 9 9 10 12 13 16 17
        let mut many = [9, 17, 3, 16, 13, 10, 1, 5, 7, 12, 4, 8, 9, 0];

        let first = kth_smallest(&mut many, 1);
        let third = kth_smallest(&mut many, 3);
        let sixth = kth_smallest(&mut many, 6);
        let fourteenth = kth_smallest(&mut many, 14);

        assert_eq!(0, first.unwrap());
        assert_eq!(3, third.unwrap());
        assert_eq!(7, sixth.unwrap());
        assert_eq!(17, fourteenth.unwrap());
    }
}
}

线性搜索

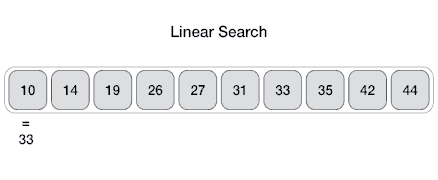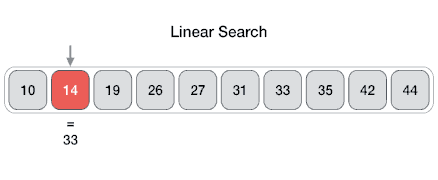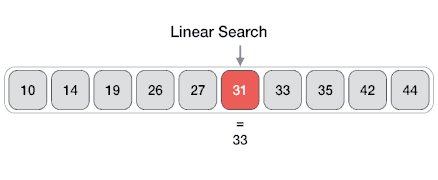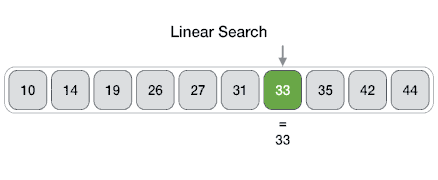
From Wikipedia: linear search or sequential search is a method for finding a target value within a list. It sequentially checks each element of the list for the target value until a match is found or until all the elements have been searched. Linear search runs in at worst linear time and makes at most n comparisons, where n is the length of the list.

Properties

• Worst case performance O(n)
• Best case performance O(1)
• Average case performance O(n)
• Worst case space complexity O(1) iterative

#![allow(unused)]
fn main() {
use std::cmp::PartialEq;

pub fn linear_search<T: PartialEq>(item: &T, arr: &[T]) -> Option<usize> {
    for (i, data) in arr.iter().enumerate() {
        if item == data {
            return Some(i);
        }
    }

    None
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn search_strings() {
        let index = linear_search(&"a", &vec!["a", "b", "c", "d", "google", "zoo"]);
        assert_eq!(index, Some(0));
    }

    #[test]
    fn search_ints() {
        let index = linear_search(&4, &vec![1, 2, 3, 4]);
        assert_eq!(index, Some(3));

        let index = linear_search(&3, &vec![1, 2, 3, 4]);
        assert_eq!(index, Some(2));

        let index = linear_search(&2, &vec![1, 2, 3, 4]);
        assert_eq!(index, Some(1));

        let index = linear_search(&1, &vec![1, 2, 3, 4]);
        assert_eq!(index, Some(0));
    }

    #[test]
    fn not_found() {
        let index = linear_search(&5, &vec![1, 2, 3, 4]);
        assert_eq!(index, None);
    }

    #[test]
    fn empty() {
        let index = linear_search(&1, &vec![]);
        assert_eq!(index, None);
    }
}
}

图论

图论算法在计算机科学中扮演着很重要的角色，它提供了对很多问题都有效的一种简单而系统的建模方式。很多问题都可以转化为图论问题，然后用图论的基本算法加以解决。

最短路径-Bellman Ford

#![allow(unused)]
fn main() {
use std::collections::BTreeMap;
use std::ops::Add;

use std::ops::Neg;

type Graph<V, E> = BTreeMap<V, BTreeMap<V, E>>;

// performs the Bellman-Ford algorithm on the given graph from the given start
// the graph is an undirected graph
//
// if there is a negative weighted loop it returns None
// else it returns a map that for each reachable vertex associates the distance and the predecessor
// since the start has no predecessor but is reachable, map[start] will be None
pub fn bellman_ford<
    V: Ord + Copy,
    E: Ord + Copy + Add<Output = E> + Neg<Output = E> + std::ops::Sub<Output = E>,
>(
    graph: &Graph<V, E>,
    start: &V,
) -> Option<BTreeMap<V, Option<(V, E)>>> {
    let mut ans: BTreeMap<V, Option<(V, E)>> = BTreeMap::new();

    ans.insert(*start, None);

    for _ in 1..(graph.len()) {
        for (u, edges) in graph {
            let dist_u = match ans.get(u) {
                Some(Some((_, d))) => Some(*d),
                Some(None) => None,
                None => continue,
            };

            for (v, d) in edges {
                match ans.get(v) {
                    Some(Some((_, dist)))
                        // if this is a longer path, do nothing
                        if match dist_u {
                            Some(dist_u) => dist_u + *d >= *dist,
                            None => d >= dist,
                        } => {}
                    Some(None) => {
                        match dist_u {
                            // if dist_u + d < 0 there is a negative loop going by start
                            // else it's just a longer path
                            Some(dist_u) if dist_u >= -*d => {}
                            // negative self edge or negative loop
                            _ => {
                                if *d > *d + *d {
                                    return None;
                                }
                            }
                        };
                    }
                    // it's a shorter path: either dist_v was infinite or it was longer than dist_u + d
                    _ => {
                        ans.insert(
                            *v,
                            Some((
                                *u,
                                match dist_u {
                                    Some(dist) => dist + *d,
                                    None => *d,
                                },
                            )),
                        );
                    }
                }
            }
        }
    }

    for (u, edges) in graph {
        for (v, d) in edges {
            match (ans.get(u), ans.get(v)) {
                (Some(None), Some(None)) if *d > *d + *d => return None,
                (Some(None), Some(Some((_, dv)))) if d < dv => return None,
                (Some(Some((_, du))), Some(None)) if *du < -*d => return None,
                (Some(Some((_, du))), Some(Some((_, dv)))) if *du + *d < *dv => return None,
                (_, _) => {}
            }
        }
    }

    Some(ans)
}

#[cfg(test)]
mod tests {
    use super::{bellman_ford, Graph};
    use std::collections::BTreeMap;

    fn add_edge<V: Ord + Copy, E: Ord>(graph: &mut Graph<V, E>, v1: V, v2: V, c: E) {
        graph.entry(v1).or_insert_with(BTreeMap::new).insert(v2, c);
        graph.entry(v2).or_insert_with(BTreeMap::new);
    }

    #[test]
    fn single_vertex() {
        let mut graph: Graph<isize, isize> = BTreeMap::new();
        graph.insert(0, BTreeMap::new());

        let mut dists = BTreeMap::new();
        dists.insert(0, None);

        assert_eq!(bellman_ford(&graph, &0), Some(dists));
    }

    #[test]
    fn single_edge() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, 0, 1, 2);

        let mut dists_0 = BTreeMap::new();
        dists_0.insert(0, None);
        dists_0.insert(1, Some((0, 2)));

        assert_eq!(bellman_ford(&graph, &0), Some(dists_0));

        let mut dists_1 = BTreeMap::new();
        dists_1.insert(1, None);

        assert_eq!(bellman_ford(&graph, &1), Some(dists_1));
    }

    #[test]
    fn tree_1() {
        let mut graph = BTreeMap::new();
        let mut dists = BTreeMap::new();
        dists.insert(1, None);
        for i in 1..100 {
            add_edge(&mut graph, i, i * 2, i * 2);
            add_edge(&mut graph, i, i * 2 + 1, i * 2 + 1);

            match dists[&i] {
                Some((_, d)) => {
                    dists.insert(i * 2, Some((i, d + i * 2)));
                    dists.insert(i * 2 + 1, Some((i, d + i * 2 + 1)));
                }
                None => {
                    dists.insert(i * 2, Some((i, i * 2)));
                    dists.insert(i * 2 + 1, Some((i, i * 2 + 1)));
                }
            }
        }

        assert_eq!(bellman_ford(&graph, &1), Some(dists));
    }

    #[test]
    fn graph_1() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, 'a', 'c', 12);
        add_edge(&mut graph, 'a', 'd', 60);
        add_edge(&mut graph, 'b', 'a', 10);
        add_edge(&mut graph, 'c', 'b', 20);
        add_edge(&mut graph, 'c', 'd', 32);
        add_edge(&mut graph, 'e', 'a', 7);

        let mut dists_a = BTreeMap::new();
        dists_a.insert('a', None);
        dists_a.insert('c', Some(('a', 12)));
        dists_a.insert('d', Some(('c', 44)));
        dists_a.insert('b', Some(('c', 32)));
        assert_eq!(bellman_ford(&graph, &'a'), Some(dists_a));

        let mut dists_b = BTreeMap::new();
        dists_b.insert('b', None);
        dists_b.insert('a', Some(('b', 10)));
        dists_b.insert('c', Some(('a', 22)));
        dists_b.insert('d', Some(('c', 54)));
        assert_eq!(bellman_ford(&graph, &'b'), Some(dists_b));

        let mut dists_c = BTreeMap::new();
        dists_c.insert('c', None);
        dists_c.insert('b', Some(('c', 20)));
        dists_c.insert('d', Some(('c', 32)));
        dists_c.insert('a', Some(('b', 30)));
        assert_eq!(bellman_ford(&graph, &'c'), Some(dists_c));

        let mut dists_d = BTreeMap::new();
        dists_d.insert('d', None);
        assert_eq!(bellman_ford(&graph, &'d'), Some(dists_d));

        let mut dists_e = BTreeMap::new();
        dists_e.insert('e', None);
        dists_e.insert('a', Some(('e', 7)));
        dists_e.insert('c', Some(('a', 19)));
        dists_e.insert('d', Some(('c', 51)));
        dists_e.insert('b', Some(('c', 39)));
        assert_eq!(bellman_ford(&graph, &'e'), Some(dists_e));
    }

    #[test]
    fn graph_2() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, 0, 1, 6);
        add_edge(&mut graph, 0, 3, 7);
        add_edge(&mut graph, 1, 2, 5);
        add_edge(&mut graph, 1, 3, 8);
        add_edge(&mut graph, 1, 4, -4);
        add_edge(&mut graph, 2, 1, -2);
        add_edge(&mut graph, 3, 2, -3);
        add_edge(&mut graph, 3, 4, 9);
        add_edge(&mut graph, 4, 0, 3);
        add_edge(&mut graph, 4, 2, 7);

        let mut dists_0 = BTreeMap::new();
        dists_0.insert(0, None);
        dists_0.insert(1, Some((2, 2)));
        dists_0.insert(2, Some((3, 4)));
        dists_0.insert(3, Some((0, 7)));
        dists_0.insert(4, Some((1, -2)));
        assert_eq!(bellman_ford(&graph, &0), Some(dists_0));

        let mut dists_1 = BTreeMap::new();
        dists_1.insert(0, Some((4, -1)));
        dists_1.insert(1, None);
        dists_1.insert(2, Some((4, 3)));
        dists_1.insert(3, Some((0, 6)));
        dists_1.insert(4, Some((1, -4)));
        assert_eq!(bellman_ford(&graph, &1), Some(dists_1));

        let mut dists_2 = BTreeMap::new();
        dists_2.insert(0, Some((4, -3)));
        dists_2.insert(1, Some((2, -2)));
        dists_2.insert(2, None);
        dists_2.insert(3, Some((0, 4)));
        dists_2.insert(4, Some((1, -6)));
        assert_eq!(bellman_ford(&graph, &2), Some(dists_2));

        let mut dists_3 = BTreeMap::new();
        dists_3.insert(0, Some((4, -6)));
        dists_3.insert(1, Some((2, -5)));
        dists_3.insert(2, Some((3, -3)));
        dists_3.insert(3, None);
        dists_3.insert(4, Some((1, -9)));
        assert_eq!(bellman_ford(&graph, &3), Some(dists_3));

        let mut dists_4 = BTreeMap::new();
        dists_4.insert(0, Some((4, 3)));
        dists_4.insert(1, Some((2, 5)));
        dists_4.insert(2, Some((4, 7)));
        dists_4.insert(3, Some((0, 10)));
        dists_4.insert(4, None);
        assert_eq!(bellman_ford(&graph, &4), Some(dists_4));
    }

    #[test]
    fn graph_with_negative_loop() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, 0, 1, 6);
        add_edge(&mut graph, 0, 3, 7);
        add_edge(&mut graph, 1, 2, 5);
        add_edge(&mut graph, 1, 3, 8);
        add_edge(&mut graph, 1, 4, -4);
        add_edge(&mut graph, 2, 1, -4);
        add_edge(&mut graph, 3, 2, -3);
        add_edge(&mut graph, 3, 4, 9);
        add_edge(&mut graph, 4, 0, 3);
        add_edge(&mut graph, 4, 2, 7);

        assert_eq!(bellman_ford(&graph, &0), None);
        assert_eq!(bellman_ford(&graph, &1), None);
        assert_eq!(bellman_ford(&graph, &2), None);
        assert_eq!(bellman_ford(&graph, &3), None);
        assert_eq!(bellman_ford(&graph, &4), None);
    }
}
}

最短路径-Dijkstra

#![allow(unused)]
fn main() {
use std::cmp::Reverse;
use std::collections::{BTreeMap, BinaryHeap};
use std::ops::Add;

type Graph<V, E> = BTreeMap<V, BTreeMap<V, E>>;

// performs Dijsktra's algorithm on the given graph from the given start
// the graph is a positively-weighted undirected graph
//
// returns a map that for each reachable vertex associates the distance and the predecessor
// since the start has no predecessor but is reachable, map[start] will be None
pub fn dijkstra<V: Ord + Copy, E: Ord + Copy + Add<Output = E>>(
    graph: &Graph<V, E>,
    start: &V,
) -> BTreeMap<V, Option<(V, E)>> {
    let mut ans = BTreeMap::new();
    let mut prio = BinaryHeap::new();

    // start is the special case that doesn't have a predecessor
    ans.insert(*start, None);

    for (new, weight) in &graph[start] {
        ans.insert(*new, Some((*start, *weight)));
        prio.push(Reverse((*weight, new, start)));
    }

    while let Some(Reverse((dist_new, new, prev))) = prio.pop() {
        match ans[new] {
            // what we popped is what is in ans, we'll compute it
            Some((p, d)) if p == *prev && d == dist_new => {}
            // otherwise it's not interesting
            _ => continue,
        }

        for (next, weight) in &graph[new] {
            match ans.get(next) {
                // if ans[next] is a lower dist than the alternative one, we do nothing
                Some(Some((_, dist_next))) if dist_new + *weight >= *dist_next => {}
                // if ans[next] is None then next is start and so the distance won't be changed, it won't be added again in prio
                Some(None) => {}
                // the new path is shorter, either new was not in ans or it was farther
                _ => {
                    ans.insert(*next, Some((*new, *weight + dist_new)));
                    prio.push(Reverse((*weight + dist_new, next, new)));
                }
            }
        }
    }

    ans
}

#[cfg(test)]
mod tests {
    use super::{dijkstra, Graph};
    use std::collections::BTreeMap;

    fn add_edge<V: Ord + Copy, E: Ord>(graph: &mut Graph<V, E>, v1: V, v2: V, c: E) {
        graph.entry(v1).or_insert_with(BTreeMap::new).insert(v2, c);
        graph.entry(v2).or_insert_with(BTreeMap::new);
    }

    #[test]
    fn single_vertex() {
        let mut graph: Graph<usize, usize> = BTreeMap::new();
        graph.insert(0, BTreeMap::new());

        let mut dists = BTreeMap::new();
        dists.insert(0, None);

        assert_eq!(dijkstra(&graph, &0), dists);
    }

    #[test]
    fn single_edge() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, 0, 1, 2);

        let mut dists_0 = BTreeMap::new();
        dists_0.insert(0, None);
        dists_0.insert(1, Some((0, 2)));

        assert_eq!(dijkstra(&graph, &0), dists_0);

        let mut dists_1 = BTreeMap::new();
        dists_1.insert(1, None);

        assert_eq!(dijkstra(&graph, &1), dists_1);
    }

    #[test]
    fn tree_1() {
        let mut graph = BTreeMap::new();
        let mut dists = BTreeMap::new();
        dists.insert(1, None);
        for i in 1..100 {
            add_edge(&mut graph, i, i * 2, i * 2);
            add_edge(&mut graph, i, i * 2 + 1, i * 2 + 1);

            match dists[&i] {
                Some((_, d)) => {
                    dists.insert(i * 2, Some((i, d + i * 2)));
                    dists.insert(i * 2 + 1, Some((i, d + i * 2 + 1)));
                }
                None => {
                    dists.insert(i * 2, Some((i, i * 2)));
                    dists.insert(i * 2 + 1, Some((i, i * 2 + 1)));
                }
            }
        }

        assert_eq!(dijkstra(&graph, &1), dists);
    }

    #[test]
    fn graph_1() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, 'a', 'c', 12);
        add_edge(&mut graph, 'a', 'd', 60);
        add_edge(&mut graph, 'b', 'a', 10);
        add_edge(&mut graph, 'c', 'b', 20);
        add_edge(&mut graph, 'c', 'd', 32);
        add_edge(&mut graph, 'e', 'a', 7);

        let mut dists_a = BTreeMap::new();
        dists_a.insert('a', None);
        dists_a.insert('c', Some(('a', 12)));
        dists_a.insert('d', Some(('c', 44)));
        dists_a.insert('b', Some(('c', 32)));
        assert_eq!(dijkstra(&graph, &'a'), dists_a);

        let mut dists_b = BTreeMap::new();
        dists_b.insert('b', None);
        dists_b.insert('a', Some(('b', 10)));
        dists_b.insert('c', Some(('a', 22)));
        dists_b.insert('d', Some(('c', 54)));
        assert_eq!(dijkstra(&graph, &'b'), dists_b);

        let mut dists_c = BTreeMap::new();
        dists_c.insert('c', None);
        dists_c.insert('b', Some(('c', 20)));
        dists_c.insert('d', Some(('c', 32)));
        dists_c.insert('a', Some(('b', 30)));
        assert_eq!(dijkstra(&graph, &'c'), dists_c);

        let mut dists_d = BTreeMap::new();
        dists_d.insert('d', None);
        assert_eq!(dijkstra(&graph, &'d'), dists_d);

        let mut dists_e = BTreeMap::new();
        dists_e.insert('e', None);
        dists_e.insert('a', Some(('e', 7)));
        dists_e.insert('c', Some(('a', 19)));
        dists_e.insert('d', Some(('c', 51)));
        dists_e.insert('b', Some(('c', 39)));
        assert_eq!(dijkstra(&graph, &'e'), dists_e);
    }
}
}

深度优先搜索

#![allow(unused)]
fn main() {
use std::collections::HashSet;
use std::collections::VecDeque;

// Perform a Depth First Search Algorithm to find a element in a graph
//
// Return a Optional with a vector with history of vertex visiteds
// or a None if the element not exists on the graph
pub fn depth_first_search(graph: &Graph, root: Vertex, objective: Vertex) -> Option<Vec<u32>> {
    let mut visited: HashSet<Vertex> = HashSet::new();
    let mut history: Vec<u32> = Vec::new();
    let mut queue = VecDeque::new();
    queue.push_back(root);

    // While there is an element in the queue
    // get the first element of the vertex queue
    while let Some(current_vertex) = queue.pop_front() {
        // Added current vertex in the history of visiteds vertex
        history.push(current_vertex.value());

        // Verify if this vertex is the objective
        if current_vertex == objective {
            // Return the Optional with the history of visiteds vertex
            return Some(history);
        }

        // For each over the neighbors of current vertex
        for neighbor in current_vertex.neighbors(graph).into_iter().rev() {
            // Insert in the HashSet of visiteds if this value not exist yet
            if visited.insert(neighbor) {
                // Add the neighbor on front of queue
                queue.push_front(neighbor);
            }
        }
    }

    // If all vertex is visited and the objective is not found
    // return a Optional with None value
    None
}

// Data Structures

#[derive(Copy, Clone, PartialEq, Eq, Hash)]
pub struct Vertex(u32);
#[derive(Copy, Clone, PartialEq, Eq, Hash)]
pub struct Edge(u32, u32);
#[derive(Clone)]
pub struct Graph {
    vertices: Vec<Vertex>,
    edges: Vec<Edge>,
}

impl Graph {
    pub fn new(vertices: Vec<Vertex>, edges: Vec<Edge>) -> Self {
        Graph { vertices, edges }
    }
}

impl From<u32> for Vertex {
    fn from(item: u32) -> Self {
        Vertex(item)
    }
}

impl Vertex {
    pub fn value(&self) -> u32 {
        self.0
    }

    pub fn neighbors(&self, graph: &Graph) -> VecDeque<Vertex> {
        graph
            .edges
            .iter()
            .filter(|e| e.0 == self.0)
            .map(|e| e.1.into())
            .collect()
    }
}

impl From<(u32, u32)> for Edge {
    fn from(item: (u32, u32)) -> Self {
        Edge(item.0, item.1)
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn find_1_fail() {
        let vertices = vec![1, 2, 3, 4, 5, 6, 7];
        let edges = vec![(1, 2), (1, 3), (2, 4), (2, 5), (3, 6), (3, 7)];

        let root = 1;
        let objective = 99;

        let graph = Graph::new(
            vertices.into_iter().map(|v| v.into()).collect(),
            edges.into_iter().map(|e| e.into()).collect(),
        );

        assert_eq!(
            depth_first_search(&graph, root.into(), objective.into()),
            None
        );
    }

    #[test]
    fn find_1_sucess() {
        let vertices = vec![1, 2, 3, 4, 5, 6, 7];
        let edges = vec![(1, 2), (1, 3), (2, 4), (2, 5), (3, 6), (3, 7)];

        let root = 1;
        let objective = 7;

        let correct_path = vec![1, 2, 4, 5, 3, 6, 7];

        let graph = Graph::new(
            vertices.into_iter().map(|v| v.into()).collect(),
            edges.into_iter().map(|e| e.into()).collect(),
        );

        assert_eq!(
            depth_first_search(&graph, root.into(), objective.into()),
            Some(correct_path)
        );
    }

    #[test]
    fn find_2_sucess() {
        let vertices = vec![0, 1, 2, 3, 4, 5, 6, 7];
        let edges = vec![
            (0, 1),
            (1, 3),
            (3, 2),
            (2, 1),
            (3, 4),
            (4, 5),
            (5, 7),
            (7, 6),
            (6, 4),
        ];

        let root = 0;
        let objective = 6;

        let correct_path = vec![0, 1, 3, 2, 4, 5, 7, 6];

        let graph = Graph::new(
            vertices.into_iter().map(|v| v.into()).collect(),
            edges.into_iter().map(|e| e.into()).collect(),
        );

        assert_eq!(
            depth_first_search(&graph, root.into(), objective.into()),
            Some(correct_path)
        );
    }

    #[test]
    fn find_3_sucess() {
        let vertices = vec![0, 1, 2, 3, 4, 5, 6, 7];
        let edges = vec![
            (0, 1),
            (1, 3),
            (3, 2),
            (2, 1),
            (3, 4),
            (4, 5),
            (5, 7),
            (7, 6),
            (6, 4),
        ];

        let root = 0;
        let objective = 4;

        let correct_path = vec![0, 1, 3, 2, 4];

        let graph = Graph::new(
            vertices.into_iter().map(|v| v.into()).collect(),
            edges.into_iter().map(|e| e.into()).collect(),
        );

        assert_eq!(
            depth_first_search(&graph, root.into(), objective.into()),
            Some(correct_path)
        );
    }
}
}

广度优先搜索

#![allow(unused)]
fn main() {
use std::collections::HashSet;
use std::collections::VecDeque;

/// Perform a breadth-first search on Graph `graph`.
///
/// # Parameters
///
/// - `graph`: The graph to search.
/// - `root`: The starting node of the graph from which to begin searching.
/// - `target`: The target node for the search.
///
/// # Returns
///
/// If the target is found, an Optional vector is returned with the history
/// of nodes visited as its contents.
///
/// If the target is not found or there is no path from the root,
/// `None` is returned.
///
pub fn breadth_first_search(graph: &Graph, root: Node, target: Node) -> Option<Vec<u32>> {
    let mut visited: HashSet<Node> = HashSet::new();
    let mut history: Vec<u32> = Vec::new();
    let mut queue = VecDeque::new();

    visited.insert(root);
    queue.push_back(root);
    while let Some(currentnode) = queue.pop_front() {
        history.push(currentnode.value());

        // If we reach the goal, return our travel history.
        if currentnode == target {
            return Some(history);
        }

        // Check the neighboring nodes for any that we've not visited yet.
        for neighbor in currentnode.neighbors(graph) {
            if !visited.contains(&neighbor) {
                visited.insert(neighbor);
                queue.push_back(neighbor);
            }
        }
    }

    // All nodes were visited, yet the target was not found.
    None
}

// Data Structures

#[derive(Copy, Clone, PartialEq, Eq, Hash)]
pub struct Node(u32);

#[derive(Copy, Clone, PartialEq, Eq, Hash)]
pub struct Edge(u32, u32);

#[derive(Clone)]
pub struct Graph {
    nodes: Vec<Node>,
    edges: Vec<Edge>,
}

impl Graph {
    pub fn new(nodes: Vec<Node>, edges: Vec<Edge>) -> Self {
        Graph { nodes, edges }
    }
}

impl From<u32> for Node {
    fn from(item: u32) -> Self {
        Node(item)
    }
}

impl Node {
    pub fn value(&self) -> u32 {
        self.0
    }

    pub fn neighbors(&self, graph: &Graph) -> Vec<Node> {
        graph
            .edges
            .iter()
            .filter(|e| e.0 == self.0)
            .map(|e| e.1.into())
            .collect()
    }
}

impl From<(u32, u32)> for Edge {
    fn from(item: (u32, u32)) -> Self {
        Edge(item.0, item.1)
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    /* Example graph #1:
     *
     *            (1)   <--- Root
     *           /   \
     *         (2)   (3)
     *        / |     | \
     *     (4) (5)   (6) (7)
     *          |
     *         (8)
     */
    fn graph1() -> Graph {
        let nodes = vec![1, 2, 3, 4, 5, 6, 7];
        let edges = vec![(1, 2), (1, 3), (2, 4), (2, 5), (3, 6), (3, 7), (5, 8)];

        Graph::new(
            nodes.into_iter().map(|v| v.into()).collect(),
            edges.into_iter().map(|e| e.into()).collect(),
        )
    }

    #[test]
    fn breadth_first_search_graph1_when_node_not_found_returns_none() {
        let graph = graph1();
        let root = 1;
        let target = 10;

        assert_eq!(
            breadth_first_search(&graph, root.into(), target.into()),
            None
        );
    }

    #[test]
    fn breadth_first_search_graph1_when_target_8_should_evaluate_all_nodes_first() {
        let graph = graph1();
        let root = 1;
        let target = 8;

        let expected_path = vec![1, 2, 3, 4, 5, 6, 7, 8];

        assert_eq!(
            breadth_first_search(&graph, root.into(), target.into()),
            Some(expected_path)
        );
    }

    /* Example graph #2:
     *
     *     (1) --- (2)     (3) --- (4)
     *            / |     /       /
     *          /   |   /       /
     *        /     | /       /
     *     (5)     (6) --- (7)     (8)
     */
    fn graph2() -> Graph {
        let nodes = vec![1, 2, 3, 4, 5, 6, 7, 8];
        let undirected_edges = vec![
            (1, 2),
            (2, 1),
            (2, 5),
            (5, 2),
            (2, 6),
            (6, 2),
            (3, 4),
            (4, 3),
            (3, 6),
            (6, 3),
            (4, 7),
            (7, 4),
            (6, 7),
            (7, 6),
        ];

        Graph::new(
            nodes.into_iter().map(|v| v.into()).collect(),
            undirected_edges.into_iter().map(|e| e.into()).collect(),
        )
    }

    #[test]
    fn breadth_first_search_graph2_when_no_path_to_node_returns_none() {
        let graph = graph2();
        let root = 8;
        let target = 4;

        assert_eq!(
            breadth_first_search(&graph, root.into(), target.into()),
            None
        );
    }

    #[test]
    fn breadth_first_search_graph2_should_find_path_from_4_to_1() {
        let graph = graph2();
        let root = 4;
        let target = 1;

        let expected_path = vec![4, 3, 7, 6, 2, 1];

        assert_eq!(
            breadth_first_search(&graph, root.into(), target.into()),
            Some(expected_path)
        );
    }
}
}

深度优先Tic Tac Toe

#[allow(unused_imports)]
use std::io;

//Interactive Tic-Tac-Toe play needs the "rand = "0.8.3" crate.
//#[cfg(not(test))]
//extern crate rand;
//#[cfg(not(test))]
//use rand::Rng;

#[derive(Copy, Clone, PartialEq, Debug)]
struct Position {
    x: u8,
    y: u8,
}

#[derive(Copy, Clone, PartialEq, Debug)]
pub enum Players {
    Blank,
    PlayerX,
    PlayerO,
}

#[derive(Copy, Clone, PartialEq, Debug)]
struct SinglePlayAction {
    position: Position,
    side: Players,
}

#[derive(Clone, PartialEq, Debug)]
pub struct PlayActions {
    positions: Vec<Position>,
    side: Players,
}

#[allow(dead_code)]
#[cfg(not(test))]
fn main() {
    let mut board = vec![vec![Players::Blank; 3]; 3];

    while !available_positions(&board).is_empty()
        && !win_check(Players::PlayerX, &board)
        && !win_check(Players::PlayerO, &board)
    {
        display_board(&board);
        println!("Type in coordinate for X mark to be played. ie. a1 etc.");
        let mut input = String::new();
        io::stdin()
            .read_line(&mut input)
            .expect("Failed to read line");

        let mut move_position: Option<Position> = None;
        input.make_ascii_lowercase();
        let bytes = input.trim().trim_start().as_bytes();
        if bytes.len() as u32 == 2
            && (bytes[0] as char).is_alphabetic()
            && (bytes[1] as char).is_numeric()
        {
            let column: u8 = bytes[0] - b'a';
            let row: u8 = bytes[1] - b'1';

            if column <= 2 && row <= 2 {
                move_position = Some(Position { x: column, y: row });
            }
        }

        //Take the validated user input coordinate and use it.
        if let Some(move_pos) = move_position {
            let open_positions = available_positions(&board);

            let mut search = open_positions.iter();
            let result = search.find(|&&x| x == move_pos);
            if result.is_none() {
                println!("Not a valid empty coordinate.");
                continue;
            } else {
                board[move_pos.y as usize][move_pos.x as usize] = Players::PlayerX;

                if win_check(Players::PlayerX, &board) {
                    display_board(&board);
                    println!("Player X Wins!");
                    return;
                }
            }

            //Find the best game plays from the current board state
            let recusion_result = minimax(Players::PlayerO, &board);
            match recusion_result {
                Some(x) => {
                    //Interactive Tic-Tac-Toe play needs the "rand = "0.8.3" crate.
                    //#[cfg(not(test))]
                    //let random_selection = rand::thread_rng().gen_range(0..x.positions.len());
                    let random_selection = 0;

                    let response_pos = x.positions[random_selection];
                    board[response_pos.y as usize][response_pos.x as usize] = Players::PlayerO;
                    if win_check(Players::PlayerO, &board) {
                        display_board(&board);
                        println!("Player O Wins!");
                        return;
                    }
                }

                None => {
                    display_board(&board);
                    println!("Draw game.");
                    return;
                }
            }
        }
    }
}

#[allow(dead_code)]
fn display_board(board: &[Vec<Players>]) {
    println!();
    for (y, board_row) in board.iter().enumerate() {
        print!("{} ", (y + 1));
        for board_cell in board_row {
            match board_cell {
                Players::PlayerX => print!("X "),
                Players::PlayerO => print!("O "),
                Players::Blank => print!("_ "),
            }
        }
        println!();
    }
    println!("  a b c");
}

fn available_positions(board: &[Vec<Players>]) -> Vec<Position> {
    let mut available: Vec<Position> = Vec::new();
    for (y, board_row) in board.iter().enumerate() {
        for (x, board_cell) in board_row.iter().enumerate() {
            if *board_cell == Players::Blank {
                available.push(Position {
                    x: x as u8,
                    y: y as u8,
                });
            }
        }
    }
    available
}

fn win_check(player: Players, board: &[Vec<Players>]) -> bool {
    if player == Players::Blank {
        return false;
    }

    //Check for a win on the diagonals.
    if (board[0][0] == board[1][1]) && (board[1][1] == board[2][2]) && (board[2][2] == player)
        || (board[2][0] == board[1][1]) && (board[1][1] == board[0][2]) && (board[0][2] == player)
    {
        return true;
    }

    for i in 0..3 {
        //Check for a win on the horizontals.
        if (board[i][0] == board[i][1]) && (board[i][1] == board[i][2]) && (board[i][2] == player) {
            return true;
        }

        //Check for a win on the verticals.
        if (board[0][i] == board[1][i]) && (board[1][i] == board[2][i]) && (board[2][i] == player) {
            return true;
        }
    }

    false
}

//Minimize the actions of the opponent while maximizing the game state of the current player.
pub fn minimax(side: Players, board: &[Vec<Players>]) -> Option<PlayActions> {
    //Check that board is in a valid state.
    if win_check(Players::PlayerX, board) || win_check(Players::PlayerO, board) {
        return None;
    }

    let opposite = match side {
        Players::PlayerX => Players::PlayerO,
        Players::PlayerO => Players::PlayerX,
        Players::Blank => panic!("Minimax can't operate when a player isn't specified."),
    };

    let positions = available_positions(board);
    if positions.is_empty() {
        return None;
    }

    //Play position
    let mut best_move: Option<PlayActions> = None;

    for pos in positions {
        let mut board_next = board.to_owned();
        board_next[pos.y as usize][pos.x as usize] = side;

        //Check for a win condition before recursion to determine if this node is terminal.
        if win_check(Players::PlayerX, &board_next) {
            append_playaction(
                side,
                &mut best_move,
                SinglePlayAction {
                    position: pos,
                    side: Players::PlayerX,
                },
            );
            continue;
        }

        if win_check(Players::PlayerO, &board_next) {
            append_playaction(
                side,
                &mut best_move,
                SinglePlayAction {
                    position: pos,
                    side: Players::PlayerO,
                },
            );
            continue;
        }

        let result = minimax(opposite, &board_next);
        let current_score = match result {
            Some(x) => x.side,
            _ => Players::Blank,
        };

        append_playaction(
            side,
            &mut best_move,
            SinglePlayAction {
                position: pos,
                side: current_score,
            },
        )
    }
    best_move
}

//Promote only better or collate equally scored game plays
fn append_playaction(
    current_side: Players,
    opt_play_actions: &mut Option<PlayActions>,
    appendee: SinglePlayAction,
) {
    if opt_play_actions.is_none() {
        *opt_play_actions = Some(PlayActions {
            positions: vec![appendee.position],
            side: appendee.side,
        });
        return;
    }

    let mut play_actions = opt_play_actions.as_mut().unwrap();

    //New game action is scored from the current side and the current saved best score against the new game action.
    match (current_side, play_actions.side, appendee.side) {
        (Players::Blank, _, _) => panic!("Unreachable state."),

        //Winning scores
        (Players::PlayerX, Players::PlayerX, Players::PlayerX) => {
            play_actions.positions.push(appendee.position);
        }
        (Players::PlayerX, Players::PlayerX, _) => {}
        (Players::PlayerO, Players::PlayerO, Players::PlayerO) => {
            play_actions.positions.push(appendee.position);
        }
        (Players::PlayerO, Players::PlayerO, _) => {}

        //Non-winning to Winning scores
        (Players::PlayerX, _, Players::PlayerX) => {
            play_actions.side = Players::PlayerX;
            play_actions.positions.clear();
            play_actions.positions.push(appendee.position);
        }
        (Players::PlayerO, _, Players::PlayerO) => {
            play_actions.side = Players::PlayerO;
            play_actions.positions.clear();
            play_actions.positions.push(appendee.position);
        }

        //Losing to Neutral scores
        (Players::PlayerX, Players::PlayerO, Players::Blank) => {
            play_actions.side = Players::Blank;
            play_actions.positions.clear();
            play_actions.positions.push(appendee.position);
        }

        (Players::PlayerO, Players::PlayerX, Players::Blank) => {
            play_actions.side = Players::Blank;
            play_actions.positions.clear();
            play_actions.positions.push(appendee.position);
        }

        //Ignoring lower scored plays
        (Players::PlayerX, Players::Blank, Players::PlayerO) => {}
        (Players::PlayerO, Players::Blank, Players::PlayerX) => {}

        //No change hence append only
        (_, _, _) => {
            assert!(play_actions.side == appendee.side);
            play_actions.positions.push(appendee.position);
        }
    }
}

#[cfg(test)]
mod test {
    use super::*;

    #[test]
    fn win_state_check() {
        let mut board = vec![vec![Players::Blank; 3]; 3];
        board[0][0] = Players::PlayerX;
        board[0][1] = Players::PlayerX;
        board[0][2] = Players::PlayerX;
        let responses = minimax(Players::PlayerO, &board);
        assert_eq!(responses, None);
    }

    #[test]
    fn win_state_check2() {
        let mut board = vec![vec![Players::Blank; 3]; 3];
        board[0][0] = Players::PlayerX;
        board[0][1] = Players::PlayerO;
        board[1][0] = Players::PlayerX;
        board[1][1] = Players::PlayerO;
        board[2][1] = Players::PlayerO;
        let responses = minimax(Players::PlayerO, &board);
        assert_eq!(responses, None);
    }

    #[test]
    fn block_win_move() {
        let mut board = vec![vec![Players::Blank; 3]; 3];
        board[0][0] = Players::PlayerX;
        board[0][1] = Players::PlayerX;
        board[1][2] = Players::PlayerO;
        board[2][2] = Players::PlayerO;
        let responses = minimax(Players::PlayerX, &board);
        assert_eq!(
            responses,
            Some(PlayActions {
                positions: vec![Position { x: 2, y: 0 }],
                side: Players::PlayerX
            })
        );
    }

    #[test]
    fn block_move() {
        let mut board = vec![vec![Players::Blank; 3]; 3];
        board[0][1] = Players::PlayerX;
        board[0][2] = Players::PlayerO;
        board[2][0] = Players::PlayerO;
        let responses = minimax(Players::PlayerX, &board);
        assert_eq!(
            responses,
            Some(PlayActions {
                positions: vec![Position { x: 1, y: 1 }],
                side: Players::Blank
            })
        );
    }

    #[test]
    fn expected_loss() {
        let mut board = vec![vec![Players::Blank; 3]; 3];
        board[0][0] = Players::PlayerX;
        board[0][2] = Players::PlayerO;
        board[1][0] = Players::PlayerX;
        board[2][0] = Players::PlayerO;
        board[2][2] = Players::PlayerO;
        let responses = minimax(Players::PlayerX, &board);
        assert_eq!(
            responses,
            Some(PlayActions {
                positions: vec![
                    Position { x: 1, y: 0 },
                    Position { x: 1, y: 1 },
                    Position { x: 2, y: 1 },
                    Position { x: 1, y: 2 }
                ],
                side: Players::PlayerO
            })
        );
    }
}

最小生成树

#![allow(unused)]
fn main() {
use std::vec::Vec;

#[derive(Debug)]
pub struct Edge {
    source: i64,
    destination: i64,
    cost: i64,
}

impl PartialEq for Edge {
    fn eq(&self, other: &Self) -> bool {
        self.source == other.source
            && self.destination == other.destination
            && self.cost == other.cost
    }
}

impl Eq for Edge {}

impl Edge {
    fn new(source: i64, destination: i64, cost: i64) -> Self {
        Self {
            source,
            destination,
            cost,
        }
    }
}

fn make_sets(number_of_vertices: i64) -> Vec<i64> {
    let mut parent: Vec<i64> = Vec::with_capacity(number_of_vertices as usize);
    for i in 0..number_of_vertices {
        parent.push(i);
    }
    parent
}

fn find(parent: &mut Vec<i64>, x: i64) -> i64 {
    let idx: usize = x as usize;
    if parent[idx] != x {
        parent[idx] = find(parent, parent[idx]);
    }
    parent[idx]
}

fn merge(parent: &mut Vec<i64>, x: i64, y: i64) {
    let idx_x: usize = find(parent, x) as usize;
    let parent_y: i64 = find(parent, y);
    parent[idx_x] = parent_y;
}

fn is_same_set(parent: &mut Vec<i64>, x: i64, y: i64) -> bool {
    find(parent, x) == find(parent, y)
}

pub fn kruskal(mut edges: Vec<Edge>, number_of_vertices: i64) -> (i64, Vec<Edge>) {
    let mut parent: Vec<i64> = make_sets(number_of_vertices);

    edges.sort_unstable_by(|a, b| a.cost.cmp(&b.cost));
    let mut total_cost: i64 = 0;
    let mut final_edges: Vec<Edge> = Vec::new();
    let mut merge_count: i64 = 0;
    for edge in edges.iter() {
        if merge_count >= number_of_vertices - 1 {
            break;
        }

        let source: i64 = edge.source;
        let destination: i64 = edge.destination;
        if !is_same_set(&mut parent, source, destination) {
            merge(&mut parent, source, destination);
            merge_count += 1;
            let cost: i64 = edge.cost;
            total_cost += cost;
            let final_edge: Edge = Edge::new(source, destination, cost);
            final_edges.push(final_edge);
        }
    }
    (total_cost, final_edges)
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_seven_vertices_eleven_edges() {
        let mut edges: Vec<Edge> = Vec::new();
        edges.push(Edge::new(0, 1, 7));
        edges.push(Edge::new(0, 3, 5));
        edges.push(Edge::new(1, 2, 8));
        edges.push(Edge::new(1, 3, 9));
        edges.push(Edge::new(1, 4, 7));
        edges.push(Edge::new(2, 4, 5));
        edges.push(Edge::new(3, 4, 15));
        edges.push(Edge::new(3, 5, 6));
        edges.push(Edge::new(4, 5, 8));
        edges.push(Edge::new(4, 6, 9));
        edges.push(Edge::new(5, 6, 11));

        let number_of_vertices: i64 = 7;

        let expected_total_cost = 39;
        let mut expected_used_edges: Vec<Edge> = Vec::new();
        expected_used_edges.push(Edge::new(0, 3, 5));
        expected_used_edges.push(Edge::new(2, 4, 5));
        expected_used_edges.push(Edge::new(3, 5, 6));
        expected_used_edges.push(Edge::new(0, 1, 7));
        expected_used_edges.push(Edge::new(1, 4, 7));
        expected_used_edges.push(Edge::new(4, 6, 9));

        let (actual_total_cost, actual_final_edges) = kruskal(edges, number_of_vertices);

        assert_eq!(actual_total_cost, expected_total_cost);
        assert_eq!(actual_final_edges, expected_used_edges);
    }

    #[test]
    fn test_ten_vertices_twenty_edges() {
        let mut edges: Vec<Edge> = Vec::new();
        edges.push(Edge::new(0, 1, 3));
        edges.push(Edge::new(0, 3, 6));
        edges.push(Edge::new(0, 4, 9));
        edges.push(Edge::new(1, 2, 2));
        edges.push(Edge::new(1, 3, 4));
        edges.push(Edge::new(1, 4, 9));
        edges.push(Edge::new(2, 3, 2));
        edges.push(Edge::new(2, 5, 8));
        edges.push(Edge::new(2, 6, 9));
        edges.push(Edge::new(3, 6, 9));
        edges.push(Edge::new(4, 5, 8));
        edges.push(Edge::new(4, 9, 18));
        edges.push(Edge::new(5, 6, 7));
        edges.push(Edge::new(5, 8, 9));
        edges.push(Edge::new(5, 9, 10));
        edges.push(Edge::new(6, 7, 4));
        edges.push(Edge::new(6, 8, 5));
        edges.push(Edge::new(7, 8, 1));
        edges.push(Edge::new(7, 9, 4));
        edges.push(Edge::new(8, 9, 3));

        let number_of_vertices: i64 = 10;

        let expected_total_cost = 38;
        let mut expected_used_edges = Vec::new();
        expected_used_edges.push(Edge::new(7, 8, 1));
        expected_used_edges.push(Edge::new(1, 2, 2));
        expected_used_edges.push(Edge::new(2, 3, 2));
        expected_used_edges.push(Edge::new(0, 1, 3));
        expected_used_edges.push(Edge::new(8, 9, 3));
        expected_used_edges.push(Edge::new(6, 7, 4));
        expected_used_edges.push(Edge::new(5, 6, 7));
        expected_used_edges.push(Edge::new(2, 5, 8));
        expected_used_edges.push(Edge::new(4, 5, 8));

        let (actual_total_cost, actual_final_edges) = kruskal(edges, number_of_vertices);

        assert_eq!(actual_total_cost, expected_total_cost);
        assert_eq!(actual_final_edges, expected_used_edges);
    }
}
}

Prim算法(最小生成树)

#![allow(unused)]
fn main() {
use std::cmp::Reverse;
use std::collections::{BTreeMap, BinaryHeap};
use std::ops::Add;

type Graph<V, E> = BTreeMap<V, BTreeMap<V, E>>;

fn add_edge<V: Ord + Copy, E: Ord + Add + Copy>(graph: &mut Graph<V, E>, v1: V, v2: V, c: E) {
    graph.entry(v1).or_insert_with(BTreeMap::new).insert(v2, c);
    graph.entry(v2).or_insert_with(BTreeMap::new).insert(v1, c);
}

// selects a start and run the algorithm from it
pub fn prim<V: Ord + Copy + std::fmt::Debug, E: Ord + Add + Copy + std::fmt::Debug>(
    graph: &Graph<V, E>,
) -> Graph<V, E> {
    match graph.keys().next() {
        Some(v) => prim_with_start(graph, *v),
        None => BTreeMap::new(),
    }
}

// only works for a connected graph
// if the given graph is not connected it will return the MST of the connected subgraph
pub fn prim_with_start<V: Ord + Copy, E: Ord + Add + Copy>(
    graph: &Graph<V, E>,
    start: V,
) -> Graph<V, E> {
    // will contain the MST
    let mut mst: Graph<V, E> = Graph::new();
    // a priority queue based on a binary heap, used to get the cheapest edge
    // the elements are an edge: the cost, destination and source
    let mut prio = BinaryHeap::new();

    mst.insert(start, BTreeMap::new());

    for (v, c) in &graph[&start] {
        // the heap is a max heap, we have to use Reverse when adding to simulate a min heap
        prio.push(Reverse((*c, v, start)));
    }

    while let Some(Reverse((dist, t, prev))) = prio.pop() {
        // the destination of the edge has already been seen
        if mst.contains_key(t) {
            continue;
        }

        // the destination is a new vertex
        add_edge(&mut mst, prev, *t, dist);

        for (v, c) in &graph[t] {
            if !mst.contains_key(v) {
                prio.push(Reverse((*c, v, *t)));
            }
        }
    }

    mst
}

#[cfg(test)]
mod tests {
    use super::{add_edge, prim, Graph};
    use std::collections::BTreeMap;

    #[test]
    fn empty() {
        assert_eq!(prim::<usize, usize>(&BTreeMap::new()), BTreeMap::new());
    }

    #[test]
    fn single_vertex() {
        let mut graph: Graph<usize, usize> = BTreeMap::new();
        graph.insert(42, BTreeMap::new());

        assert_eq!(prim(&graph), graph);
    }

    #[test]
    fn single_edge() {
        let mut graph = BTreeMap::new();

        add_edge(&mut graph, 42, 666, 12);

        assert_eq!(prim(&graph), graph);
    }

    #[test]
    fn tree_1() {
        let mut graph = BTreeMap::new();

        add_edge(&mut graph, 0, 1, 10);
        add_edge(&mut graph, 0, 2, 11);
        add_edge(&mut graph, 2, 3, 12);
        add_edge(&mut graph, 2, 4, 13);
        add_edge(&mut graph, 1, 5, 14);
        add_edge(&mut graph, 1, 6, 15);
        add_edge(&mut graph, 3, 7, 16);

        assert_eq!(prim(&graph), graph);
    }

    #[test]
    fn tree_2() {
        let mut graph = BTreeMap::new();

        add_edge(&mut graph, 1, 2, 11);
        add_edge(&mut graph, 2, 3, 12);
        add_edge(&mut graph, 2, 4, 13);
        add_edge(&mut graph, 4, 5, 14);
        add_edge(&mut graph, 4, 6, 15);
        add_edge(&mut graph, 6, 7, 16);

        assert_eq!(prim(&graph), graph);
    }

    #[test]
    fn tree_3() {
        let mut graph = BTreeMap::new();

        for i in 1..100 {
            add_edge(&mut graph, i, 2 * i, i);
            add_edge(&mut graph, i, 2 * i + 1, -i);
        }

        assert_eq!(prim(&graph), graph);
    }

    #[test]
    fn graph_1() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, 'a', 'b', 6);
        add_edge(&mut graph, 'a', 'c', 7);
        add_edge(&mut graph, 'a', 'e', 2);
        add_edge(&mut graph, 'a', 'f', 3);
        add_edge(&mut graph, 'b', 'c', 5);
        add_edge(&mut graph, 'c', 'e', 5);
        add_edge(&mut graph, 'd', 'e', 4);
        add_edge(&mut graph, 'd', 'f', 1);
        add_edge(&mut graph, 'e', 'f', 2);

        let mut ans = BTreeMap::new();
        add_edge(&mut ans, 'd', 'f', 1);
        add_edge(&mut ans, 'e', 'f', 2);
        add_edge(&mut ans, 'a', 'e', 2);
        add_edge(&mut ans, 'b', 'c', 5);
        add_edge(&mut ans, 'c', 'e', 5);

        assert_eq!(prim(&graph), ans);
    }

    #[test]
    fn graph_2() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, 1, 2, 6);
        add_edge(&mut graph, 1, 3, 1);
        add_edge(&mut graph, 1, 4, 5);
        add_edge(&mut graph, 2, 3, 5);
        add_edge(&mut graph, 2, 5, 3);
        add_edge(&mut graph, 3, 4, 5);
        add_edge(&mut graph, 3, 5, 6);
        add_edge(&mut graph, 3, 6, 4);
        add_edge(&mut graph, 4, 6, 2);
        add_edge(&mut graph, 5, 6, 6);

        let mut ans = BTreeMap::new();
        add_edge(&mut ans, 1, 3, 1);
        add_edge(&mut ans, 4, 6, 2);
        add_edge(&mut ans, 2, 5, 3);
        add_edge(&mut ans, 2, 3, 5);
        add_edge(&mut ans, 3, 6, 4);

        assert_eq!(prim(&graph), ans);
    }

    #[test]
    fn graph_3() {
        let mut graph = BTreeMap::new();
        add_edge(&mut graph, "v1", "v2", 1);
        add_edge(&mut graph, "v1", "v3", 3);
        add_edge(&mut graph, "v1", "v5", 6);
        add_edge(&mut graph, "v2", "v3", 2);
        add_edge(&mut graph, "v2", "v4", 3);
        add_edge(&mut graph, "v2", "v5", 5);
        add_edge(&mut graph, "v3", "v4", 5);
        add_edge(&mut graph, "v3", "v6", 2);
        add_edge(&mut graph, "v4", "v5", 2);
        add_edge(&mut graph, "v4", "v6", 4);
        add_edge(&mut graph, "v5", "v6", 1);

        let mut ans = BTreeMap::new();
        add_edge(&mut ans, "v1", "v2", 1);
        add_edge(&mut ans, "v5", "v6", 1);
        add_edge(&mut ans, "v2", "v3", 2);
        add_edge(&mut ans, "v3", "v6", 2);
        add_edge(&mut ans, "v4", "v5", 2);

        assert_eq!(prim(&graph), ans);
    }
}
}

动态规划

动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。 动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

斐波那契(fibonacci)

#![allow(unused)]
fn main() {
/// Fibonacci via Dynamic Programming

/// fibonacci(n) returns the nth fibonacci number
/// This function uses the definition of Fibonacci where:
/// F(0) = F(1) = 1 and F(n+1) = F(n) + F(n-1) for n>0
///
/// Warning: This will overflow the 128-bit unsigned integer at n=186
pub fn fibonacci(n: u32) -> u128 {
    // Use a and b to store the previous two values in the sequence
    let mut a = 0;
    let mut b = 1;
    for _i in 0..n {
        // As we iterate through, move b's value into a and the new computed
        // value into b.
        let c = a + b;
        a = b;
        b = c;
    }
    b
}

/// fibonacci(n) returns the nth fibonacci number
/// This function uses the definition of Fibonacci where:
/// F(0) = F(1) = 1 and F(n+1) = F(n) + F(n-1) for n>0
///
/// Warning: This will overflow the 128-bit unsigned integer at n=186
pub fn recursive_fibonacci(n: u32) -> u128 {
    // Call the actual tail recursive implementation, with the extra
    // arguments set up.
    _recursive_fibonacci(n, 0, 1)
}

fn _recursive_fibonacci(n: u32, previous: u128, current: u128) -> u128 {
    if n == 0 {
        current
    } else {
        _recursive_fibonacci(n - 1, current, current + previous)
    }
}

/// classical_fibonacci(n) returns the nth fibonacci number
/// This function uses the definition of Fibonacci where:
/// F(0) = 0, F(1) = 1 and F(n+1) = F(n) + F(n-1) for n>0
///
/// Warning: This will overflow the 128-bit unsigned integer at n=186
pub fn classical_fibonacci(n: u32) -> u128 {
    match n {
        0 => 0,
        1 => 1,
        _ => {
            let k = n / 2;
            let f1 = classical_fibonacci(k);
            let f2 = classical_fibonacci(k - 1);

            match n % 4 {
                0 | 2 => f1 * (f1 + 2 * f2),
                1 => (2 * f1 + f2) * (2 * f1 - f2) + 2,
                _ => (2 * f1 + f2) * (2 * f1 - f2) - 2,
            }
        }
    }
}

/// logarithmic_fibonacci(n) returns the nth fibonacci number
/// This function uses the definition of Fibonacci where:
/// F(0) = 0, F(1) = 1 and F(n+1) = F(n) + F(n-1) for n>0
///
/// Warning: This will overflow the 128-bit unsigned integer at n=186
pub fn logarithmic_fibonacci(n: u32) -> u128 {
    // if it is the max value before overflow, use n-1 then get the second
    // value in the tuple
    if n == 186 {
        let (_, second) = _logarithmic_fibonacci(185);
        second
    } else {
        let (first, _) = _logarithmic_fibonacci(n);
        first
    }
}

fn _logarithmic_fibonacci(n: u32) -> (u128, u128) {
    match n {
        0 => (0, 1),
        _ => {
            let (current, next) = _logarithmic_fibonacci(n / 2);
            let c = current * (next * 2 - current);
            let d = current * current + next * next;

            match n % 2 {
                0 => (c, d),
                _ => (d, c + d),
            }
        }
    }
}

#[cfg(test)]
mod tests {
    use super::classical_fibonacci;
    use super::fibonacci;
    use super::logarithmic_fibonacci;
    use super::recursive_fibonacci;

    #[test]
    fn test_fibonacci() {
        assert_eq!(fibonacci(0), 1);
        assert_eq!(fibonacci(1), 1);
        assert_eq!(fibonacci(2), 2);
        assert_eq!(fibonacci(3), 3);
        assert_eq!(fibonacci(4), 5);
        assert_eq!(fibonacci(5), 8);
        assert_eq!(fibonacci(10), 89);
        assert_eq!(fibonacci(20), 10946);
        assert_eq!(fibonacci(100), 573147844013817084101);
        assert_eq!(fibonacci(184), 205697230343233228174223751303346572685);
    }

    #[test]
    fn test_recursive_fibonacci() {
        assert_eq!(recursive_fibonacci(0), 1);
        assert_eq!(recursive_fibonacci(1), 1);
        assert_eq!(recursive_fibonacci(2), 2);
        assert_eq!(recursive_fibonacci(3), 3);
        assert_eq!(recursive_fibonacci(4), 5);
        assert_eq!(recursive_fibonacci(5), 8);
        assert_eq!(recursive_fibonacci(10), 89);
        assert_eq!(recursive_fibonacci(20), 10946);
        assert_eq!(recursive_fibonacci(100), 573147844013817084101);
        assert_eq!(
            recursive_fibonacci(184),
            205697230343233228174223751303346572685
        );
    }

    #[test]
    fn test_classical_fibonacci() {
        assert_eq!(classical_fibonacci(0), 0);
        assert_eq!(classical_fibonacci(1), 1);
        assert_eq!(classical_fibonacci(2), 1);
        assert_eq!(classical_fibonacci(3), 2);
        assert_eq!(classical_fibonacci(4), 3);
        assert_eq!(classical_fibonacci(5), 5);
        assert_eq!(classical_fibonacci(10), 55);
        assert_eq!(classical_fibonacci(20), 6765);
        assert_eq!(classical_fibonacci(21), 10946);
        assert_eq!(classical_fibonacci(100), 354224848179261915075);
        assert_eq!(
            classical_fibonacci(184),
            127127879743834334146972278486287885163
        );
    }

    #[test]
    fn test_logarithmic_fibonacci() {
        assert_eq!(logarithmic_fibonacci(0), 0);
        assert_eq!(logarithmic_fibonacci(1), 1);
        assert_eq!(logarithmic_fibonacci(2), 1);
        assert_eq!(logarithmic_fibonacci(3), 2);
        assert_eq!(logarithmic_fibonacci(4), 3);
        assert_eq!(logarithmic_fibonacci(5), 5);
        assert_eq!(logarithmic_fibonacci(10), 55);
        assert_eq!(logarithmic_fibonacci(20), 6765);
        assert_eq!(logarithmic_fibonacci(21), 10946);
        assert_eq!(logarithmic_fibonacci(100), 354224848179261915075);
        assert_eq!(
            logarithmic_fibonacci(184),
            127127879743834334146972278486287885163
        );
    }

    #[test]
    /// Check that the itterative and recursive fibonacci
    /// produce the same value. Both are combinatorial ( F(0) = F(1) = 1 )
    fn test_iterative_and_recursive_equivalence() {
        assert_eq!(fibonacci(0), recursive_fibonacci(0));
        assert_eq!(fibonacci(1), recursive_fibonacci(1));
        assert_eq!(fibonacci(2), recursive_fibonacci(2));
        assert_eq!(fibonacci(3), recursive_fibonacci(3));
        assert_eq!(fibonacci(4), recursive_fibonacci(4));
        assert_eq!(fibonacci(5), recursive_fibonacci(5));
        assert_eq!(fibonacci(10), recursive_fibonacci(10));
        assert_eq!(fibonacci(20), recursive_fibonacci(20));
        assert_eq!(fibonacci(100), recursive_fibonacci(100));
        assert_eq!(fibonacci(184), recursive_fibonacci(184));
    }

    #[test]
    /// Check that classical and combinatorial fibonacci produce the
    /// same value when 'n' differs by 1.
    /// classical fibonacci: ( F(0) = 0, F(1) = 1 )
    /// combinatorial fibonacci: ( F(0) = F(1) = 1 )
    fn test_classical_and_combinatorial_are_off_by_one() {
        assert_eq!(classical_fibonacci(1), fibonacci(0));
        assert_eq!(classical_fibonacci(2), fibonacci(1));
        assert_eq!(classical_fibonacci(3), fibonacci(2));
        assert_eq!(classical_fibonacci(4), fibonacci(3));
        assert_eq!(classical_fibonacci(5), fibonacci(4));
        assert_eq!(classical_fibonacci(6), fibonacci(5));
        assert_eq!(classical_fibonacci(11), fibonacci(10));
        assert_eq!(classical_fibonacci(20), fibonacci(19));
        assert_eq!(classical_fibonacci(21), fibonacci(20));
        assert_eq!(classical_fibonacci(101), fibonacci(100));
        assert_eq!(classical_fibonacci(185), fibonacci(184));
    }
}
}

找钱(Coin change)

#![allow(unused)]
fn main() {
/// Coin change via Dynamic Programming

/// coin_change(coins, amount) returns the fewest number of coins that need to make up that amount.
/// If that amount of money cannot be made up by any combination of the coins, return `None`.
///
/// Arguments:
///     * `coins` - coins of different denominations
///     * `amount` - a total amount of money be made up.
/// Complexity
///     - time complexity: O(amount * coins.length),
///     - space complexity: O(amount),
pub fn coin_change(coins: &[usize], amount: usize) -> Option<usize> {
    let mut dp = vec![std::usize::MAX; amount + 1];
    dp[0] = 0;

    // Assume dp[i] is the fewest number of coins making up amount i,
    // then for every coin in coins, dp[i] = min(dp[i - coin] + 1).
    for i in 0..=amount {
        for j in 0..coins.len() {
            if i >= coins[j] && dp[i - coins[j]] != std::usize::MAX {
                dp[i] = dp[i].min(dp[i - coins[j]] + 1);
            }
        }
    }

    match dp[amount] {
        std::usize::MAX => None,
        _ => Some(dp[amount]),
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        // 11 = 5 * 2 + 1 * 1
        let coins = vec![1, 2, 5];
        assert_eq!(Some(3), coin_change(&coins, 11));

        // 119 = 11 * 10 + 7 * 1 + 2 * 1
        let coins = vec![2, 3, 5, 7, 11];
        assert_eq!(Some(12), coin_change(&coins, 119));
    }

    #[test]
    fn coins_empty() {
        let coins = vec![];
        assert_eq!(None, coin_change(&coins, 1));
    }

    #[test]
    fn amount_zero() {
        let coins = vec![1, 2, 3];
        assert_eq!(Some(0), coin_change(&coins, 0));
    }

    #[test]
    fn fail_change() {
        // 3 can't be change by 2.
        let coins = vec![2];
        assert_eq!(None, coin_change(&coins, 3));
        let coins = vec![10, 20, 50, 100];
        assert_eq!(None, coin_change(&coins, 5));
    }
}
}

最小编辑距离(Edit distance)

#![allow(unused)]
fn main() {
/// Coin change via Dynamic Programming

/// coin_change(coins, amount) returns the fewest number of coins that need to make up that amount.
/// If that amount of money cannot be made up by any combination of the coins, return `None`.
///
/// Arguments:
///     * `coins` - coins of different denominations
///     * `amount` - a total amount of money be made up.
/// Complexity
///     - time complexity: O(amount * coins.length),
///     - space complexity: O(amount),
pub fn coin_change(coins: &[usize], amount: usize) -> Option<usize> {
    let mut dp = vec![std::usize::MAX; amount + 1];
    dp[0] = 0;

    // Assume dp[i] is the fewest number of coins making up amount i,
    // then for every coin in coins, dp[i] = min(dp[i - coin] + 1).
    for i in 0..=amount {
        for j in 0..coins.len() {
            if i >= coins[j] && dp[i - coins[j]] != std::usize::MAX {
                dp[i] = dp[i].min(dp[i - coins[j]] + 1);
            }
        }
    }

    match dp[amount] {
        std::usize::MAX => None,
        _ => Some(dp[amount]),
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        // 11 = 5 * 2 + 1 * 1
        let coins = vec![1, 2, 5];
        assert_eq!(Some(3), coin_change(&coins, 11));

        // 119 = 11 * 10 + 7 * 1 + 2 * 1
        let coins = vec![2, 3, 5, 7, 11];
        assert_eq!(Some(12), coin_change(&coins, 119));
    }

    #[test]
    fn coins_empty() {
        let coins = vec![];
        assert_eq!(None, coin_change(&coins, 1));
    }

    #[test]
    fn amount_zero() {
        let coins = vec![1, 2, 3];
        assert_eq!(Some(0), coin_change(&coins, 0));
    }

    #[test]
    fn fail_change() {
        // 3 can't be change by 2.
        let coins = vec![2];
        assert_eq!(None, coin_change(&coins, 3));
        let coins = vec![10, 20, 50, 100];
        assert_eq!(None, coin_change(&coins, 5));
    }
}
}

扔鸡蛋(Egg dropping)

#![allow(unused)]
fn main() {
/// # Egg Dropping Puzzle

/// `egg_drop(eggs, floors)` returns the least number of egg droppings
///     required to determine the highest floor from which an egg will not
///     break upon dropping
///
/// Assumptions: n > 0
pub fn egg_drop(eggs: u32, floors: u32) -> u32 {
    assert!(eggs > 0);

    // Explicity handle edge cases (optional)
    if eggs == 1 || floors == 0 || floors == 1 {
        return floors;
    }

    let eggs_index = eggs as usize;
    let floors_index = floors as usize;

    // Store solutions to subproblems in 2D Vec,
    // where egg_drops[i][j] represents the solution to the egg dropping
    // problem with i eggs and j floors
    let mut egg_drops: Vec<Vec<u32>> = vec![vec![0; floors_index + 1]; eggs_index + 1];

    // Assign solutions for egg_drop(n, 0) = 0, egg_drop(n, 1) = 1
    for egg_drop in egg_drops.iter_mut().skip(1) {
        egg_drop[0] = 0;
        egg_drop[1] = 1;
    }

    // Assign solutions to egg_drop(1, k) = k
    for j in 1..=floors_index {
        egg_drops[1][j] = j as u32;
    }

    // Complete solutions vector using optimal substructure property
    for i in 2..=eggs_index {
        for j in 2..=floors_index {
            egg_drops[i][j] = std::u32::MAX;

            for k in 1..=j {
                let res = 1 + std::cmp::max(egg_drops[i - 1][k - 1], egg_drops[i][j - k]);

                if res < egg_drops[i][j] {
                    egg_drops[i][j] = res;
                }
            }
        }
    }

    egg_drops[eggs_index][floors_index]
}

#[cfg(test)]
mod tests {
    use super::egg_drop;

    #[test]
    fn zero_floors() {
        assert_eq!(egg_drop(5, 0), 0);
    }

    #[test]
    fn one_egg() {
        assert_eq!(egg_drop(1, 8), 8);
    }

    #[test]
    fn eggs2_floors2() {
        assert_eq!(egg_drop(2, 2), 2);
    }

    #[test]
    fn eggs3_floors5() {
        assert_eq!(egg_drop(3, 5), 3);
    }

    #[test]
    fn eggs2_floors10() {
        assert_eq!(egg_drop(2, 10), 4);
    }

    #[test]
    fn eggs2_floors36() {
        assert_eq!(egg_drop(2, 36), 8);
    }

    #[test]
    fn large_floors() {
        assert_eq!(egg_drop(2, 100), 14);
    }
}
}

判断子序列

#![allow(unused)]
fn main() {
/// Fibonacci via Dynamic Programming

/// fibonacci(n) returns the nth fibonacci number
/// This function uses the definition of Fibonacci where:
/// F(0) = F(1) = 1 and F(n+1) = F(n) + F(n-1) for n>0
///
/// Warning: This will overflow the 128-bit unsigned integer at n=186
pub fn fibonacci(n: u32) -> u128 {
    // Use a and b to store the previous two values in the sequence
    let mut a = 0;
    let mut b = 1;
    for _i in 0..n {
        // As we iterate through, move b's value into a and the new computed
        // value into b.
        let c = a + b;
        a = b;
        b = c;
    }
    b
}

/// fibonacci(n) returns the nth fibonacci number
/// This function uses the definition of Fibonacci where:
/// F(0) = F(1) = 1 and F(n+1) = F(n) + F(n-1) for n>0
///
/// Warning: This will overflow the 128-bit unsigned integer at n=186
pub fn recursive_fibonacci(n: u32) -> u128 {
    // Call the actual tail recursive implementation, with the extra
    // arguments set up.
    _recursive_fibonacci(n, 0, 1)
}

fn _recursive_fibonacci(n: u32, previous: u128, current: u128) -> u128 {
    if n == 0 {
        current
    } else {
        _recursive_fibonacci(n - 1, current, current + previous)
    }
}

/// classical_fibonacci(n) returns the nth fibonacci number
/// This function uses the definition of Fibonacci where:
/// F(0) = 0, F(1) = 1 and F(n+1) = F(n) + F(n-1) for n>0
///
/// Warning: This will overflow the 128-bit unsigned integer at n=186
pub fn classical_fibonacci(n: u32) -> u128 {
    match n {
        0 => 0,
        1 => 1,
        _ => {
            let k = n / 2;
            let f1 = classical_fibonacci(k);
            let f2 = classical_fibonacci(k - 1);

            match n % 4 {
                0 | 2 => f1 * (f1 + 2 * f2),
                1 => (2 * f1 + f2) * (2 * f1 - f2) + 2,
                _ => (2 * f1 + f2) * (2 * f1 - f2) - 2,
            }
        }
    }
}

/// logarithmic_fibonacci(n) returns the nth fibonacci number
/// This function uses the definition of Fibonacci where:
/// F(0) = 0, F(1) = 1 and F(n+1) = F(n) + F(n-1) for n>0
///
/// Warning: This will overflow the 128-bit unsigned integer at n=186
pub fn logarithmic_fibonacci(n: u32) -> u128 {
    // if it is the max value before overflow, use n-1 then get the second
    // value in the tuple
    if n == 186 {
        let (_, second) = _logarithmic_fibonacci(185);
        second
    } else {
        let (first, _) = _logarithmic_fibonacci(n);
        first
    }
}

fn _logarithmic_fibonacci(n: u32) -> (u128, u128) {
    match n {
        0 => (0, 1),
        _ => {
            let (current, next) = _logarithmic_fibonacci(n / 2);
            let c = current * (next * 2 - current);
            let d = current * current + next * next;

            match n % 2 {
                0 => (c, d),
                _ => (d, c + d),
            }
        }
    }
}

#[cfg(test)]
mod tests {
    use super::classical_fibonacci;
    use super::fibonacci;
    use super::logarithmic_fibonacci;
    use super::recursive_fibonacci;

    #[test]
    fn test_fibonacci() {
        assert_eq!(fibonacci(0), 1);
        assert_eq!(fibonacci(1), 1);
        assert_eq!(fibonacci(2), 2);
        assert_eq!(fibonacci(3), 3);
        assert_eq!(fibonacci(4), 5);
        assert_eq!(fibonacci(5), 8);
        assert_eq!(fibonacci(10), 89);
        assert_eq!(fibonacci(20), 10946);
        assert_eq!(fibonacci(100), 573147844013817084101);
        assert_eq!(fibonacci(184), 205697230343233228174223751303346572685);
    }

    #[test]
    fn test_recursive_fibonacci() {
        assert_eq!(recursive_fibonacci(0), 1);
        assert_eq!(recursive_fibonacci(1), 1);
        assert_eq!(recursive_fibonacci(2), 2);
        assert_eq!(recursive_fibonacci(3), 3);
        assert_eq!(recursive_fibonacci(4), 5);
        assert_eq!(recursive_fibonacci(5), 8);
        assert_eq!(recursive_fibonacci(10), 89);
        assert_eq!(recursive_fibonacci(20), 10946);
        assert_eq!(recursive_fibonacci(100), 573147844013817084101);
        assert_eq!(
            recursive_fibonacci(184),
            205697230343233228174223751303346572685
        );
    }

    #[test]
    fn test_classical_fibonacci() {
        assert_eq!(classical_fibonacci(0), 0);
        assert_eq!(classical_fibonacci(1), 1);
        assert_eq!(classical_fibonacci(2), 1);
        assert_eq!(classical_fibonacci(3), 2);
        assert_eq!(classical_fibonacci(4), 3);
        assert_eq!(classical_fibonacci(5), 5);
        assert_eq!(classical_fibonacci(10), 55);
        assert_eq!(classical_fibonacci(20), 6765);
        assert_eq!(classical_fibonacci(21), 10946);
        assert_eq!(classical_fibonacci(100), 354224848179261915075);
        assert_eq!(
            classical_fibonacci(184),
            127127879743834334146972278486287885163
        );
    }

    #[test]
    fn test_logarithmic_fibonacci() {
        assert_eq!(logarithmic_fibonacci(0), 0);
        assert_eq!(logarithmic_fibonacci(1), 1);
        assert_eq!(logarithmic_fibonacci(2), 1);
        assert_eq!(logarithmic_fibonacci(3), 2);
        assert_eq!(logarithmic_fibonacci(4), 3);
        assert_eq!(logarithmic_fibonacci(5), 5);
        assert_eq!(logarithmic_fibonacci(10), 55);
        assert_eq!(logarithmic_fibonacci(20), 6765);
        assert_eq!(logarithmic_fibonacci(21), 10946);
        assert_eq!(logarithmic_fibonacci(100), 354224848179261915075);
        assert_eq!(
            logarithmic_fibonacci(184),
            127127879743834334146972278486287885163
        );
    }

    #[test]
    /// Check that the itterative and recursive fibonacci
    /// produce the same value. Both are combinatorial ( F(0) = F(1) = 1 )
    fn test_iterative_and_recursive_equivalence() {
        assert_eq!(fibonacci(0), recursive_fibonacci(0));
        assert_eq!(fibonacci(1), recursive_fibonacci(1));
        assert_eq!(fibonacci(2), recursive_fibonacci(2));
        assert_eq!(fibonacci(3), recursive_fibonacci(3));
        assert_eq!(fibonacci(4), recursive_fibonacci(4));
        assert_eq!(fibonacci(5), recursive_fibonacci(5));
        assert_eq!(fibonacci(10), recursive_fibonacci(10));
        assert_eq!(fibonacci(20), recursive_fibonacci(20));
        assert_eq!(fibonacci(100), recursive_fibonacci(100));
        assert_eq!(fibonacci(184), recursive_fibonacci(184));
    }

    #[test]
    /// Check that classical and combinatorial fibonacci produce the
    /// same value when 'n' differs by 1.
    /// classical fibonacci: ( F(0) = 0, F(1) = 1 )
    /// combinatorial fibonacci: ( F(0) = F(1) = 1 )
    fn test_classical_and_combinatorial_are_off_by_one() {
        assert_eq!(classical_fibonacci(1), fibonacci(0));
        assert_eq!(classical_fibonacci(2), fibonacci(1));
        assert_eq!(classical_fibonacci(3), fibonacci(2));
        assert_eq!(classical_fibonacci(4), fibonacci(3));
        assert_eq!(classical_fibonacci(5), fibonacci(4));
        assert_eq!(classical_fibonacci(6), fibonacci(5));
        assert_eq!(classical_fibonacci(11), fibonacci(10));
        assert_eq!(classical_fibonacci(20), fibonacci(19));
        assert_eq!(classical_fibonacci(21), fibonacci(20));
        assert_eq!(classical_fibonacci(101), fibonacci(100));
        assert_eq!(classical_fibonacci(185), fibonacci(184));
    }
}
}

背包问题

#![allow(unused)]
fn main() {
//! Solves the knapsack problem
use std::cmp::max;

/// knapsack_table(w, weights, values) returns the knapsack table (`n`, `m`) with maximum values, where `n` is number of items
///
/// Arguments:
///     * `w` - knapsack capacity
///     * `weights` - set of weights for each item
///     * `values` - set of values for each item
fn knapsack_table(w: &usize, weights: &[usize], values: &[usize]) -> Vec<Vec<usize>> {
    // Initialize `n` - number of items
    let n: usize = weights.len();
    // Initialize `m`
    // m[i, w] - the maximum value that can be attained with weight less that or equal to `w` using items up to `i`
    let mut m: Vec<Vec<usize>> = vec![vec![0; w + 1]; n + 1];

    for i in 0..=n {
        for j in 0..=*w {
            // m[i, j] compiled according to the following rule:
            if i == 0 || j == 0 {
                m[i][j] = 0;
            } else if weights[i - 1] <= j {
                // If `i` is in the knapsack
                // Then m[i, j] is equal to the maximum value of the knapsack,
                // where the weight `j` is reduced by the weight of the `i-th` item and the set of admissible items plus the value `k`
                m[i][j] = max(values[i - 1] + m[i - 1][j - weights[i - 1]], m[i - 1][j]);
            } else {
                // If the item `i` did not get into the knapsack
                // Then m[i, j] is equal to the maximum cost of a knapsack with the same capacity and a set of admissible items
                m[i][j] = m[i - 1][j]
            }
        }
    }
    m
}

/// knapsack_items(weights, m, i, j) returns the indices of the items of the optimal knapsack (from 1 to `n`)
///
/// Arguments:
///     * `weights` - set of weights for each item
///     * `m` - knapsack table with maximum values
///     * `i` - include items 1 through `i` in knapsack (for the initial value, use `n`)
///     * `j` - maximum weight of the knapsack
fn knapsack_items(weights: &[usize], m: &[Vec<usize>], i: usize, j: usize) -> Vec<usize> {
    if i == 0 {
        return vec![];
    }
    if m[i][j] > m[i - 1][j] {
        let mut knap: Vec<usize> = knapsack_items(weights, m, i - 1, j - weights[i - 1]);
        knap.push(i);
        knap
    } else {
        knapsack_items(weights, m, i - 1, j)
    }
}

/// knapsack(w, weights, values) returns the tuple where first value is `optimal profit`,
/// second value is `knapsack optimal weight` and the last value is `indices of items`, that we got (from 1 to `n`)
///
/// Arguments:
///     * `w` - knapsack capacity
///     * `weights` - set of weights for each item
///     * `values` - set of values for each item
///
/// Complexity
///     - time complexity: O(nw),
///     - space complexity: O(nw),
///
/// where `n` and `w` are `number of items` and `knapsack capacity`
pub fn knapsack(w: usize, weights: Vec<usize>, values: Vec<usize>) -> (usize, usize, Vec<usize>) {
    // Checks if the number of items in the list of weights is the same as the number of items in the list of values
    assert_eq!(weights.len(), values.len(), "Number of items in the list of weights doesn't match the number of items in the list of values!");
    // Initialize `n` - number of items
    let n: usize = weights.len();
    // Find the knapsack table
    let m: Vec<Vec<usize>> = knapsack_table(&w, &weights, &values);
    // Find the indices of the items
    let items: Vec<usize> = knapsack_items(&weights, &m, n, w);
    // Find the total weight of optimal knapsack
    let mut total_weight: usize = 0;
    for i in items.iter() {
        total_weight += weights[i - 1];
    }
    // Return result
    (m[n][w], total_weight, items)
}

#[cfg(test)]
mod tests {
    // Took test datasets from https://people.sc.fsu.edu/~jburkardt/datasets/bin_packing/bin_packing.html
    use super::*;

    #[test]
    fn test_p02() {
        assert_eq!(
            (51, 26, vec![2, 3, 4]),
            knapsack(26, vec![12, 7, 11, 8, 9], vec![24, 13, 23, 15, 16])
        );
    }

    #[test]
    fn test_p04() {
        assert_eq!(
            (150, 190, vec![1, 2, 5]),
            knapsack(
                190,
                vec![56, 59, 80, 64, 75, 17],
                vec![50, 50, 64, 46, 50, 5]
            )
        );
    }

    #[test]
    fn test_p01() {
        assert_eq!(
            (309, 165, vec![1, 2, 3, 4, 6]),
            knapsack(
                165,
                vec![23, 31, 29, 44, 53, 38, 63, 85, 89, 82],
                vec![92, 57, 49, 68, 60, 43, 67, 84, 87, 72]
            )
        );
    }

    #[test]
    fn test_p06() {
        assert_eq!(
            (1735, 169, vec![2, 4, 7]),
            knapsack(
                170,
                vec![41, 50, 49, 59, 55, 57, 60],
                vec![442, 525, 511, 593, 546, 564, 617]
            )
        );
    }

    #[test]
    fn test_p07() {
        assert_eq!(
            (1458, 749, vec![1, 3, 5, 7, 8, 9, 14, 15]),
            knapsack(
                750,
                vec![70, 73, 77, 80, 82, 87, 90, 94, 98, 106, 110, 113, 115, 118, 120],
                vec![135, 139, 149, 150, 156, 163, 173, 184, 192, 201, 210, 214, 221, 229, 240]
            )
        );
    }
}
}

最长公共子序列

#![allow(unused)]
fn main() {
/// Longest common subsequence via Dynamic Programming

/// longest_common_subsequence(a, b) returns the longest common subsequence
/// between the strings a and b.
pub fn longest_common_subsequence(a: &str, b: &str) -> String {
    let a: Vec<_> = a.chars().collect();
    let b: Vec<_> = b.chars().collect();
    let (na, nb) = (a.len(), b.len());

    // solutions[i][j] is the length of the longest common subsequence
    // between a[0..i-1] and b[0..j-1]
    let mut solutions = vec![vec![0; nb + 1]; na + 1];

    for (i, ci) in a.iter().enumerate() {
        for (j, cj) in b.iter().enumerate() {
            // if ci == cj, there is a new common character;
            // otherwise, take the best of the two solutions
            // at (i-1,j) and (i,j-1)
            solutions[i + 1][j + 1] = if ci == cj {
                solutions[i][j] + 1
            } else {
                solutions[i][j + 1].max(solutions[i + 1][j])
            }
        }
    }

    // reconstitute the solution string from the lengths
    let mut result: Vec<char> = Vec::new();
    let (mut i, mut j) = (na, nb);
    while i > 0 && j > 0 {
        if a[i - 1] == b[j - 1] {
            result.push(a[i - 1]);
            i -= 1;
            j -= 1;
        } else if solutions[i - 1][j] > solutions[i][j - 1] {
            i -= 1;
        } else {
            j -= 1;
        }
    }

    result.reverse();
    result.iter().collect()
}

#[cfg(test)]
mod tests {
    use super::longest_common_subsequence;

    #[test]
    fn test_longest_common_subsequence() {
        // empty case
        assert_eq!(&longest_common_subsequence("", ""), "");
        assert_eq!(&longest_common_subsequence("", "abcd"), "");
        assert_eq!(&longest_common_subsequence("abcd", ""), "");

        // simple cases
        assert_eq!(&longest_common_subsequence("abcd", "c"), "c");
        assert_eq!(&longest_common_subsequence("abcd", "d"), "d");
        assert_eq!(&longest_common_subsequence("abcd", "e"), "");
        assert_eq!(&longest_common_subsequence("abcdefghi", "acegi"), "acegi");

        // less simple cases
        assert_eq!(&longest_common_subsequence("abcdgh", "aedfhr"), "adh");
        assert_eq!(&longest_common_subsequence("aggtab", "gxtxayb"), "gtab");

        // unicode
        assert_eq!(
            &longest_common_subsequence("你好，世界", "再见世界"),
            "世界"
        );
    }
}
}

最长连续递增序列

#![allow(unused)]
fn main() {
pub fn longest_continuous_increasing_subsequence<T: Ord>(input_array: &[T]) -> &[T] {
    let length: usize = input_array.len();

    //Handle the base cases
    if length <= 1 {
        return input_array;
    }

    //Create the array to store the longest subsequence at each location
    let mut tracking_vec = vec![1; length];

    //Iterate through the input and store longest subsequences at each location in the vector
    for i in (0..length - 1).rev() {
        if input_array[i] < input_array[i + 1] {
            tracking_vec[i] = tracking_vec[i + 1] + 1;
        }
    }

    //Find the longest subsequence
    let mut max_index: usize = 0;
    let mut max_value: i32 = 0;
    for (index, value) in tracking_vec.iter().enumerate() {
        if value > &max_value {
            max_value = *value;
            max_index = index;
        }
    }

    &input_array[max_index..max_index + max_value as usize]
}

#[cfg(test)]
mod tests {
    use super::longest_continuous_increasing_subsequence;

    #[test]
    fn test_longest_increasing_subsequence() {
        //Base Cases
        let base_case_array: [i32; 0] = [];
        assert_eq!(
            &longest_continuous_increasing_subsequence(&base_case_array),
            &[]
        );
        assert_eq!(&longest_continuous_increasing_subsequence(&[1]), &[1]);

        //Normal i32 Cases
        assert_eq!(
            &longest_continuous_increasing_subsequence(&[1, 2, 3, 4]),
            &[1, 2, 3, 4]
        );
        assert_eq!(
            &longest_continuous_increasing_subsequence(&[1, 2, 2, 3, 4, 2]),
            &[2, 3, 4]
        );
        assert_eq!(
            &longest_continuous_increasing_subsequence(&[5, 4, 3, 2, 1]),
            &[5]
        );
        assert_eq!(
            &longest_continuous_increasing_subsequence(&[5, 4, 3, 4, 2, 1]),
            &[3, 4]
        );

        //Non-Numeric case
        assert_eq!(
            &longest_continuous_increasing_subsequence(&['a', 'b', 'c']),
            &['a', 'b', 'c']
        );
        assert_eq!(
            &longest_continuous_increasing_subsequence(&['d', 'c', 'd']),
            &['c', 'd']
        );
    }
}
}

最长上升子序列

#![allow(unused)]
fn main() {
/// Finds the longest increasing subsequence and returns it.
///
/// If multiple subsequences with the longest possible subsequence length can be found, the
/// subsequence which appeared first will be returned (see `test_example_1`).
///
/// Inspired by [this LeetCode problem](https://leetcode.com/problems/longest-increasing-subsequence/).
pub fn longest_increasing_subsequence<T: Ord + Clone>(input_array: Vec<T>) -> Vec<T> {
    let n = input_array.len();
    if n <= 1 {
        return input_array;
    }

    // Find longest increasing subsequence
    let mut dp = vec![(1, None); n];
    let mut pair = 0;

    for i in 0..n {
        for j in 0..i {
            if input_array[j] < input_array[i] && dp[j].0 + 1 > dp[i].0 {
                dp[i] = (dp[j].0 + 1, Some(j));

                if dp[i].0 > dp[pair].0 {
                    pair = i;
                }
            }
        }
    }

    // Construct subsequence
    let mut out: Vec<T> = Vec::with_capacity(dp[pair].0);

    out.push(input_array[pair].clone());
    while let Some(next) = dp[pair].1 {
        pair = next;
        out.push(input_array[pair].clone());
    }

    out.into_iter().rev().collect()
}

#[cfg(test)]
mod tests {
    use super::longest_increasing_subsequence;

    #[test]
    /// Need to specify generic type T in order to function
    fn test_empty_vec() {
        assert_eq!(longest_increasing_subsequence::<i32>(vec![]), vec![]);
    }

    #[test]
    fn test_example_1() {
        assert_eq!(
            longest_increasing_subsequence(vec![10, 9, 2, 5, 3, 7, 101, 18]),
            vec![2, 5, 7, 101]
        );
    }

    #[test]
    fn test_example_2() {
        assert_eq!(
            longest_increasing_subsequence(vec![0, 1, 0, 3, 2, 3]),
            vec![0, 1, 2, 3]
        );
    }

    #[test]
    fn test_example_3() {
        assert_eq!(
            longest_increasing_subsequence(vec![7, 7, 7, 7, 7, 7, 7]),
            vec![7]
        );
    }

    #[test]
    #[ignore]
    fn test_tle() {
        assert_eq!(
            longest_increasing_subsequence(vec![
                1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23,
                24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44,
                45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65,
                66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86,
                87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105,
                106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121,
                122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137,
                138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153,
                154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169,
                170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185,
                186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201,
                202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217,
                218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233,
                234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249,
                250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265,
                266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281,
                282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297,
                298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313,
                314, 315, 316, 317, 318, 319, 320, 321, 322, 323, 324, 325, 326, 327, 328, 329,
                330, 331, 332, 333, 334, 335, 336, 337, 338, 339, 340, 341, 342, 343, 344, 345,
                346, 347, 348, 349, 350, 351, 352, 353, 354, 355, 356, 357, 358, 359, 360, 361,
                362, 363, 364, 365, 366, 367, 368, 369, 370, 371, 372, 373, 374, 375, 376, 377,
                378, 379, 380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391, 392, 393,
                394, 395, 396, 397, 398, 399, 400, 401, 402, 403, 404, 405, 406, 407, 408, 409,
                410, 411, 412, 413, 414, 415, 416, 417, 418, 419, 420, 421, 422, 423, 424, 425,
                426, 427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439, 440, 441,
                442, 443, 444, 445, 446, 447, 448, 449, 450, 451, 452, 453, 454, 455, 456, 457,
                458, 459, 460, 461, 462, 463, 464, 465, 466, 467, 468, 469, 470, 471, 472, 473,
                474, 475, 476, 477, 478, 479, 480, 481, 482, 483, 484, 485, 486, 487, 488, 489,
                490, 491, 492, 493, 494, 495, 496, 497, 498, 499, 500, 501, 502, 503, 504, 505,
                506, 507, 508, 509, 510, 511, 512, 513, 514, 515, 516, 517, 518, 519, 520, 521,
                522, 523, 524, 525, 526, 527, 528, 529, 530, 531, 532, 533, 534, 535, 536, 537,
                538, 539, 540, 541, 542, 543, 544, 545, 546, 547, 548, 549, 550, 551, 552, 553,
                554, 555, 556, 557, 558, 559, 560, 561, 562, 563, 564, 565, 566, 567, 568, 569,
                570, 571, 572, 573, 574, 575, 576, 577, 578, 579, 580, 581, 582, 583, 584, 585,
                586, 587, 588, 589, 590, 591, 592, 593, 594, 595, 596, 597, 598, 599, 600, 601,
                602, 603, 604, 605, 606, 607, 608, 609, 610, 611, 612, 613, 614, 615, 616, 617,
                618, 619, 620, 621, 622, 623, 624, 625, 626, 627, 628, 629, 630, 631, 632, 633,
                634, 635, 636, 637, 638, 639, 640, 641, 642, 643, 644, 645, 646, 647, 648, 649,
                650, 651, 652, 653, 654, 655, 656, 657, 658, 659, 660, 661, 662, 663, 664, 665,
                666, 667, 668, 669, 670, 671, 672, 673, 674, 675, 676, 677, 678, 679, 680, 681,
                682, 683, 684, 685, 686, 687, 688, 689, 690, 691, 692, 693, 694, 695, 696, 697,
                698, 699, 700, 701, 702, 703, 704, 705, 706, 707, 708, 709, 710, 711, 712, 713,
                714, 715, 716, 717, 718, 719, 720, 721, 722, 723, 724, 725, 726, 727, 728, 729,
                730, 731, 732, 733, 734, 735, 736, 737, 738, 739, 740, 741, 742, 743, 744, 745,
                746, 747, 748, 749, 750, 751, 752, 753, 754, 755, 756, 757, 758, 759, 760, 761,
                762, 763, 764, 765, 766, 767, 768, 769, 770, 771, 772, 773, 774, 775, 776, 777,
                778, 779, 780, 781, 782, 783, 784, 785, 786, 787, 788, 789, 790, 791, 792, 793,
                794, 795, 796, 797, 798, 799, 800, 801, 802, 803, 804, 805, 806, 807, 808, 809,
                810, 811, 812, 813, 814, 815, 816, 817, 818, 819, 820, 821, 822, 823, 824, 825,
                826, 827, 828, 829, 830, 831, 832, 833, 834, 835, 836, 837, 838, 839, 840, 841,
                842, 843, 844, 845, 846, 847, 848, 849, 850, 851, 852, 853, 854, 855, 856, 857,
                858, 859, 860, 861, 862, 863, 864, 865, 866, 867, 868, 869, 870, 871, 872, 873,
                874, 875, 876, 877, 878, 879, 880, 881, 882, 883, 884, 885, 886, 887, 888, 889,
                890, 891, 892, 893, 894, 895, 896, 897, 898, 899, 900, 901, 902, 903, 904, 905,
                906, 907, 908, 909, 910, 911, 912, 913, 914, 915, 916, 917, 918, 919, 920, 921,
                922, 923, 924, 925, 926, 927, 928, 929, 930, 931, 932, 933, 934, 935, 936, 937,
                938, 939, 940, 941, 942, 943, 944, 945, 946, 947, 948, 949, 950, 951, 952, 953,
                954, 955, 956, 957, 958, 959, 960, 961, 962, 963, 964, 965, 966, 967, 968, 969,
                970, 971, 972, 973, 974, 975, 976, 977, 978, 979, 980, 981, 982, 983, 984, 985,
                986, 987, 988, 989, 990, 991, 992, 993, 994, 995, 996, 997, 998, 999, 1000, 1001,
                1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010, 1011, 1012, 1013, 1014, 1015,
                1016, 1017, 1018, 1019, 1020, 1021, 1022, 1023, 1024, 1025, 1026, 1027, 1028, 1029,
                1030, 1031, 1032, 1033, 1034, 1035, 1036, 1037, 1038, 1039, 1040, 1041, 1042, 1043,
                1044, 1045, 1046, 1047, 1048, 1049, 1050, 1051, 1052, 1053, 1054, 1055, 1056, 1057,
                1058, 1059, 1060, 1061, 1062, 1063, 1064, 1065, 1066, 1067, 1068, 1069, 1070, 1071,
                1072, 1073, 1074, 1075, 1076, 1077, 1078, 1079, 1080, 1081, 1082, 1083, 1084, 1085,
                1086, 1087, 1088, 1089, 1090, 1091, 1092, 1093, 1094, 1095, 1096, 1097, 1098, 1099,
                1100, 1101, 1102, 1103, 1104, 1105, 1106, 1107, 1108, 1109, 1110, 1111, 1112, 1113,
                1114, 1115, 1116, 1117, 1118, 1119, 1120, 1121, 1122, 1123, 1124, 1125, 1126, 1127,
                1128, 1129, 1130, 1131, 1132, 1133, 1134, 1135, 1136, 1137, 1138, 1139, 1140, 1141,
                1142, 1143, 1144, 1145, 1146, 1147, 1148, 1149, 1150, 1151, 1152, 1153, 1154, 1155,
                1156, 1157, 1158, 1159, 1160, 1161, 1162, 1163, 1164, 1165, 1166, 1167, 1168, 1169,
                1170, 1171, 1172, 1173, 1174, 1175, 1176, 1177, 1178, 1179, 1180, 1181, 1182, 1183,
                1184, 1185, 1186, 1187, 1188, 1189, 1190, 1191, 1192, 1193, 1194, 1195, 1196, 1197,
                1198, 1199, 1200, 1201, 1202, 1203, 1204, 1205, 1206, 1207, 1208, 1209, 1210, 1211,
                1212, 1213, 1214, 1215, 1216, 1217, 1218, 1219, 1220, 1221, 1222, 1223, 1224, 1225,
                1226, 1227, 1228, 1229, 1230, 1231, 1232, 1233, 1234, 1235, 1236, 1237, 1238, 1239,
                1240, 1241, 1242, 1243, 1244, 1245, 1246, 1247, 1248, 1249, 1250, 1251, 1252, 1253,
                1254, 1255, 1256, 1257, 1258, 1259, 1260, 1261, 1262, 1263, 1264, 1265, 1266, 1267,
                1268, 1269, 1270, 1271, 1272, 1273, 1274, 1275, 1276, 1277, 1278, 1279, 1280, 1281,
                1282, 1283, 1284, 1285, 1286, 1287, 1288, 1289, 1290, 1291, 1292, 1293, 1294, 1295,
                1296, 1297, 1298, 1299, 1300, 1301, 1302, 1303, 1304, 1305, 1306, 1307, 1308, 1309,
                1310, 1311, 1312, 1313, 1314, 1315, 1316, 1317, 1318, 1319, 1320, 1321, 1322, 1323,
                1324, 1325, 1326, 1327, 1328, 1329, 1330, 1331, 1332, 1333, 1334, 1335, 1336, 1337,
                1338, 1339, 1340, 1341, 1342, 1343, 1344, 1345, 1346, 1347, 1348, 1349, 1350, 1351,
                1352, 1353, 1354, 1355, 1356, 1357, 1358, 1359, 1360, 1361, 1362, 1363, 1364, 1365,
                1366, 1367, 1368, 1369, 1370, 1371, 1372, 1373, 1374, 1375, 1376, 1377, 1378, 1379,
                1380, 1381, 1382, 1383, 1384, 1385, 1386, 1387, 1388, 1389, 1390, 1391, 1392, 1393,
                1394, 1395, 1396, 1397, 1398, 1399, 1400, 1401, 1402, 1403, 1404, 1405, 1406, 1407,
                1408, 1409, 1410, 1411, 1412, 1413, 1414, 1415, 1416, 1417, 1418, 1419, 1420, 1421,
                1422, 1423, 1424, 1425, 1426, 1427, 1428, 1429, 1430, 1431, 1432, 1433, 1434, 1435,
                1436, 1437, 1438, 1439, 1440, 1441, 1442, 1443, 1444, 1445, 1446, 1447, 1448, 1449,
                1450, 1451, 1452, 1453, 1454, 1455, 1456, 1457, 1458, 1459, 1460, 1461, 1462, 1463,
                1464, 1465, 1466, 1467, 1468, 1469, 1470, 1471, 1472, 1473, 1474, 1475, 1476, 1477,
                1478, 1479, 1480, 1481, 1482, 1483, 1484, 1485, 1486, 1487, 1488, 1489, 1490, 1491,
                1492, 1493, 1494, 1495, 1496, 1497, 1498, 1499, 1500, 1501, 1502, 1503, 1504, 1505,
                1506, 1507, 1508, 1509, 1510, 1511, 1512, 1513, 1514, 1515, 1516, 1517, 1518, 1519,
                1520, 1521, 1522, 1523, 1524, 1525, 1526, 1527, 1528, 1529, 1530, 1531, 1532, 1533,
                1534, 1535, 1536, 1537, 1538, 1539, 1540, 1541, 1542, 1543, 1544, 1545, 1546, 1547,
                1548, 1549, 1550, 1551, 1552, 1553, 1554, 1555, 1556, 1557, 1558, 1559, 1560, 1561,
                1562, 1563, 1564, 1565, 1566, 1567, 1568, 1569, 1570, 1571, 1572, 1573, 1574, 1575,
                1576, 1577, 1578, 1579, 1580, 1581, 1582, 1583, 1584, 1585, 1586, 1587, 1588, 1589,
                1590, 1591, 1592, 1593, 1594, 1595, 1596, 1597, 1598, 1599, 1600, 1601, 1602, 1603,
                1604, 1605, 1606, 1607, 1608, 1609, 1610, 1611, 1612, 1613, 1614, 1615, 1616, 1617,
                1618, 1619, 1620, 1621, 1622, 1623, 1624, 1625, 1626, 1627, 1628, 1629, 1630, 1631,
                1632, 1633, 1634, 1635, 1636, 1637, 1638, 1639, 1640, 1641, 1642, 1643, 1644, 1645,
                1646, 1647, 1648, 1649, 1650, 1651, 1652, 1653, 1654, 1655, 1656, 1657, 1658, 1659,
                1660, 1661, 1662, 1663, 1664, 1665, 1666, 1667, 1668, 1669, 1670, 1671, 1672, 1673,
                1674, 1675, 1676, 1677, 1678, 1679, 1680, 1681, 1682, 1683, 1684, 1685, 1686, 1687,
                1688, 1689, 1690, 1691, 1692, 1693, 1694, 1695, 1696, 1697, 1698, 1699, 1700, 1701,
                1702, 1703, 1704, 1705, 1706, 1707, 1708, 1709, 1710, 1711, 1712, 1713, 1714, 1715,
                1716, 1717, 1718, 1719, 1720, 1721, 1722, 1723, 1724, 1725, 1726, 1727, 1728, 1729,
                1730, 1731, 1732, 1733, 1734, 1735, 1736, 1737, 1738, 1739, 1740, 1741, 1742, 1743,
                1744, 1745, 1746, 1747, 1748, 1749, 1750, 1751, 1752, 1753, 1754, 1755, 1756, 1757,
                1758, 1759, 1760, 1761, 1762, 1763, 1764, 1765, 1766, 1767, 1768, 1769, 1770, 1771,
                1772, 1773, 1774, 1775, 1776, 1777, 1778, 1779, 1780, 1781, 1782, 1783, 1784, 1785,
                1786, 1787, 1788, 1789, 1790, 1791, 1792, 1793, 1794, 1795, 1796, 1797, 1798, 1799,
                1800, 1801, 1802, 1803, 1804, 1805, 1806, 1807, 1808, 1809, 1810, 1811, 1812, 1813,
                1814, 1815, 1816, 1817, 1818, 1819, 1820, 1821, 1822, 1823, 1824, 1825, 1826, 1827,
                1828, 1829, 1830, 1831, 1832, 1833, 1834, 1835, 1836, 1837, 1838, 1839, 1840, 1841,
                1842, 1843, 1844, 1845, 1846, 1847, 1848, 1849, 1850, 1851, 1852, 1853, 1854, 1855,
                1856, 1857, 1858, 1859, 1860, 1861, 1862, 1863, 1864, 1865, 1866, 1867, 1868, 1869,
                1870, 1871, 1872, 1873, 1874, 1875, 1876, 1877, 1878, 1879, 1880, 1881, 1882, 1883,
                1884, 1885, 1886, 1887, 1888, 1889, 1890, 1891, 1892, 1893, 1894, 1895, 1896, 1897,
                1898, 1899, 1900, 1901, 1902, 1903, 1904, 1905, 1906, 1907, 1908, 1909, 1910, 1911,
                1912, 1913, 1914, 1915, 1916, 1917, 1918, 1919, 1920, 1921, 1922, 1923, 1924, 1925,
                1926, 1927, 1928, 1929, 1930, 1931, 1932, 1933, 1934, 1935, 1936, 1937, 1938, 1939,
                1940, 1941, 1942, 1943, 1944, 1945, 1946, 1947, 1948, 1949, 1950, 1951, 1952, 1953,
                1954, 1955, 1956, 1957, 1958, 1959, 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967,
                1968, 1969, 1970, 1971, 1972, 1973, 1974, 1975, 1976, 1977, 1978, 1979, 1980, 1981,
                1982, 1983, 1984, 1985, 1986, 1987, 1988, 1989, 1990, 1991, 1992, 1993, 1994, 1995,
                1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009,
                2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023,
                2024, 2025, 2026, 2027, 2028, 2029, 2030, 2031, 2032, 2033, 2034, 2035, 2036, 2037,
                2038, 2039, 2040, 2041, 2042, 2043, 2044, 2045, 2046, 2047, 2048, 2049, 2050, 2051,
                2052, 2053, 2054, 2055, 2056, 2057, 2058, 2059, 2060, 2061, 2062, 2063, 2064, 2065,
                2066, 2067, 2068, 2069, 2070, 2071, 2072, 2073, 2074, 2075, 2076, 2077, 2078, 2079,
                2080, 2081, 2082, 2083, 2084, 2085, 2086, 2087, 2088, 2089, 2090, 2091, 2092, 2093,
                2094, 2095, 2096, 2097, 2098, 2099, 2100, 2101, 2102, 2103, 2104, 2105, 2106, 2107,
                2108, 2109, 2110, 2111, 2112, 2113, 2114, 2115, 2116, 2117, 2118, 2119, 2120, 2121,
                2122, 2123, 2124, 2125, 2126, 2127, 2128, 2129, 2130, 2131, 2132, 2133, 2134, 2135,
                2136, 2137, 2138, 2139, 2140, 2141, 2142, 2143, 2144, 2145, 2146, 2147, 2148, 2149,
                2150, 2151, 2152, 2153, 2154, 2155, 2156, 2157, 2158, 2159, 2160, 2161, 2162, 2163,
                2164, 2165, 2166, 2167, 2168, 2169, 2170, 2171, 2172, 2173, 2174, 2175, 2176, 2177,
                2178, 2179, 2180, 2181, 2182, 2183, 2184, 2185, 2186, 2187, 2188, 2189, 2190, 2191,
                2192, 2193, 2194, 2195, 2196, 2197, 2198, 2199, 2200, 2201, 2202, 2203, 2204, 2205,
                2206, 2207, 2208, 2209, 2210, 2211, 2212, 2213, 2214, 2215, 2216, 2217, 2218, 2219,
                2220, 2221, 2222, 2223, 2224, 2225, 2226, 2227, 2228, 2229, 2230, 2231, 2232, 2233,
                2234, 2235, 2236, 2237, 2238, 2239, 2240, 2241, 2242, 2243, 2244, 2245, 2246, 2247,
                2248, 2249, 2250, 2251, 2252, 2253, 2254, 2255, 2256, 2257, 2258, 2259, 2260, 2261,
                2262, 2263, 2264, 2265, 2266, 2267, 2268, 2269, 2270, 2271, 2272, 2273, 2274, 2275,
                2276, 2277, 2278, 2279, 2280, 2281, 2282, 2283, 2284, 2285, 2286, 2287, 2288, 2289,
                2290, 2291, 2292, 2293, 2294, 2295, 2296, 2297, 2298, 2299, 2300, 2301, 2302, 2303,
                2304, 2305, 2306, 2307, 2308, 2309, 2310, 2311, 2312, 2313, 2314, 2315, 2316, 2317,
                2318, 2319, 2320, 2321, 2322, 2323, 2324, 2325, 2326, 2327, 2328, 2329, 2330, 2331,
                2332, 2333, 2334, 2335, 2336, 2337, 2338, 2339, 2340, 2341, 2342, 2343, 2344, 2345,
                2346, 2347, 2348, 2349, 2350, 2351, 2352, 2353, 2354, 2355, 2356, 2357, 2358, 2359,
                2360, 2361, 2362, 2363, 2364, 2365, 2366, 2367, 2368, 2369, 2370, 2371, 2372, 2373,
                2374, 2375, 2376, 2377, 2378, 2379, 2380, 2381, 2382, 2383, 2384, 2385, 2386, 2387,
                2388, 2389, 2390, 2391, 2392, 2393, 2394, 2395, 2396, 2397, 2398, 2399, 2400, 2401,
                2402, 2403, 2404, 2405, 2406, 2407, 2408, 2409, 2410, 2411, 2412, 2413, 2414, 2415,
                2416, 2417, 2418, 2419, 2420, 2421, 2422, 2423, 2424, 2425, 2426, 2427, 2428, 2429,
                2430, 2431, 2432, 2433, 2434, 2435, 2436, 2437, 2438, 2439, 2440, 2441, 2442, 2443,
                2444, 2445, 2446, 2447, 2448, 2449, 2450, 2451, 2452, 2453, 2454, 2455, 2456, 2457,
                2458, 2459, 2460, 2461, 2462, 2463, 2464, 2465, 2466, 2467, 2468, 2469, 2470, 2471,
                2472, 2473, 2474, 2475, 2476, 2477, 2478, 2479, 2480, 2481, 2482, 2483, 2484, 2485,
                2486, 2487, 2488, 2489, 2490, 2491, 2492, 2493, 2494, 2495, 2496, 2497, 2498, 2499,
                2500
            ]),
            vec![
                1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23,
                24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44,
                45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65,
                66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86,
                87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105,
                106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121,
                122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137,
                138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153,
                154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169,
                170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185,
                186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201,
                202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217,
                218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233,
                234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249,
                250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265,
                266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281,
                282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297,
                298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313,
                314, 315, 316, 317, 318, 319, 320, 321, 322, 323, 324, 325, 326, 327, 328, 329,
                330, 331, 332, 333, 334, 335, 336, 337, 338, 339, 340, 341, 342, 343, 344, 345,
                346, 347, 348, 349, 350, 351, 352, 353, 354, 355, 356, 357, 358, 359, 360, 361,
                362, 363, 364, 365, 366, 367, 368, 369, 370, 371, 372, 373, 374, 375, 376, 377,
                378, 379, 380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391, 392, 393,
                394, 395, 396, 397, 398, 399, 400, 401, 402, 403, 404, 405, 406, 407, 408, 409,
                410, 411, 412, 413, 414, 415, 416, 417, 418, 419, 420, 421, 422, 423, 424, 425,
                426, 427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439, 440, 441,
                442, 443, 444, 445, 446, 447, 448, 449, 450, 451, 452, 453, 454, 455, 456, 457,
                458, 459, 460, 461, 462, 463, 464, 465, 466, 467, 468, 469, 470, 471, 472, 473,
                474, 475, 476, 477, 478, 479, 480, 481, 482, 483, 484, 485, 486, 487, 488, 489,
                490, 491, 492, 493, 494, 495, 496, 497, 498, 499, 500, 501, 502, 503, 504, 505,
                506, 507, 508, 509, 510, 511, 512, 513, 514, 515, 516, 517, 518, 519, 520, 521,
                522, 523, 524, 525, 526, 527, 528, 529, 530, 531, 532, 533, 534, 535, 536, 537,
                538, 539, 540, 541, 542, 543, 544, 545, 546, 547, 548, 549, 550, 551, 552, 553,
                554, 555, 556, 557, 558, 559, 560, 561, 562, 563, 564, 565, 566, 567, 568, 569,
                570, 571, 572, 573, 574, 575, 576, 577, 578, 579, 580, 581, 582, 583, 584, 585,
                586, 587, 588, 589, 590, 591, 592, 593, 594, 595, 596, 597, 598, 599, 600, 601,
                602, 603, 604, 605, 606, 607, 608, 609, 610, 611, 612, 613, 614, 615, 616, 617,
                618, 619, 620, 621, 622, 623, 624, 625, 626, 627, 628, 629, 630, 631, 632, 633,
                634, 635, 636, 637, 638, 639, 640, 641, 642, 643, 644, 645, 646, 647, 648, 649,
                650, 651, 652, 653, 654, 655, 656, 657, 658, 659, 660, 661, 662, 663, 664, 665,
                666, 667, 668, 669, 670, 671, 672, 673, 674, 675, 676, 677, 678, 679, 680, 681,
                682, 683, 684, 685, 686, 687, 688, 689, 690, 691, 692, 693, 694, 695, 696, 697,
                698, 699, 700, 701, 702, 703, 704, 705, 706, 707, 708, 709, 710, 711, 712, 713,
                714, 715, 716, 717, 718, 719, 720, 721, 722, 723, 724, 725, 726, 727, 728, 729,
                730, 731, 732, 733, 734, 735, 736, 737, 738, 739, 740, 741, 742, 743, 744, 745,
                746, 747, 748, 749, 750, 751, 752, 753, 754, 755, 756, 757, 758, 759, 760, 761,
                762, 763, 764, 765, 766, 767, 768, 769, 770, 771, 772, 773, 774, 775, 776, 777,
                778, 779, 780, 781, 782, 783, 784, 785, 786, 787, 788, 789, 790, 791, 792, 793,
                794, 795, 796, 797, 798, 799, 800, 801, 802, 803, 804, 805, 806, 807, 808, 809,
                810, 811, 812, 813, 814, 815, 816, 817, 818, 819, 820, 821, 822, 823, 824, 825,
                826, 827, 828, 829, 830, 831, 832, 833, 834, 835, 836, 837, 838, 839, 840, 841,
                842, 843, 844, 845, 846, 847, 848, 849, 850, 851, 852, 853, 854, 855, 856, 857,
                858, 859, 860, 861, 862, 863, 864, 865, 866, 867, 868, 869, 870, 871, 872, 873,
                874, 875, 876, 877, 878, 879, 880, 881, 882, 883, 884, 885, 886, 887, 888, 889,
                890, 891, 892, 893, 894, 895, 896, 897, 898, 899, 900, 901, 902, 903, 904, 905,
                906, 907, 908, 909, 910, 911, 912, 913, 914, 915, 916, 917, 918, 919, 920, 921,
                922, 923, 924, 925, 926, 927, 928, 929, 930, 931, 932, 933, 934, 935, 936, 937,
                938, 939, 940, 941, 942, 943, 944, 945, 946, 947, 948, 949, 950, 951, 952, 953,
                954, 955, 956, 957, 958, 959, 960, 961, 962, 963, 964, 965, 966, 967, 968, 969,
                970, 971, 972, 973, 974, 975, 976, 977, 978, 979, 980, 981, 982, 983, 984, 985,
                986, 987, 988, 989, 990, 991, 992, 993, 994, 995, 996, 997, 998, 999, 1000, 1001,
                1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010, 1011, 1012, 1013, 1014, 1015,
                1016, 1017, 1018, 1019, 1020, 1021, 1022, 1023, 1024, 1025, 1026, 1027, 1028, 1029,
                1030, 1031, 1032, 1033, 1034, 1035, 1036, 1037, 1038, 1039, 1040, 1041, 1042, 1043,
                1044, 1045, 1046, 1047, 1048, 1049, 1050, 1051, 1052, 1053, 1054, 1055, 1056, 1057,
                1058, 1059, 1060, 1061, 1062, 1063, 1064, 1065, 1066, 1067, 1068, 1069, 1070, 1071,
                1072, 1073, 1074, 1075, 1076, 1077, 1078, 1079, 1080, 1081, 1082, 1083, 1084, 1085,
                1086, 1087, 1088, 1089, 1090, 1091, 1092, 1093, 1094, 1095, 1096, 1097, 1098, 1099,
                1100, 1101, 1102, 1103, 1104, 1105, 1106, 1107, 1108, 1109, 1110, 1111, 1112, 1113,
                1114, 1115, 1116, 1117, 1118, 1119, 1120, 1121, 1122, 1123, 1124, 1125, 1126, 1127,
                1128, 1129, 1130, 1131, 1132, 1133, 1134, 1135, 1136, 1137, 1138, 1139, 1140, 1141,
                1142, 1143, 1144, 1145, 1146, 1147, 1148, 1149, 1150, 1151, 1152, 1153, 1154, 1155,
                1156, 1157, 1158, 1159, 1160, 1161, 1162, 1163, 1164, 1165, 1166, 1167, 1168, 1169,
                1170, 1171, 1172, 1173, 1174, 1175, 1176, 1177, 1178, 1179, 1180, 1181, 1182, 1183,
                1184, 1185, 1186, 1187, 1188, 1189, 1190, 1191, 1192, 1193, 1194, 1195, 1196, 1197,
                1198, 1199, 1200, 1201, 1202, 1203, 1204, 1205, 1206, 1207, 1208, 1209, 1210, 1211,
                1212, 1213, 1214, 1215, 1216, 1217, 1218, 1219, 1220, 1221, 1222, 1223, 1224, 1225,
                1226, 1227, 1228, 1229, 1230, 1231, 1232, 1233, 1234, 1235, 1236, 1237, 1238, 1239,
                1240, 1241, 1242, 1243, 1244, 1245, 1246, 1247, 1248, 1249, 1250, 1251, 1252, 1253,
                1254, 1255, 1256, 1257, 1258, 1259, 1260, 1261, 1262, 1263, 1264, 1265, 1266, 1267,
                1268, 1269, 1270, 1271, 1272, 1273, 1274, 1275, 1276, 1277, 1278, 1279, 1280, 1281,
                1282, 1283, 1284, 1285, 1286, 1287, 1288, 1289, 1290, 1291, 1292, 1293, 1294, 1295,
                1296, 1297, 1298, 1299, 1300, 1301, 1302, 1303, 1304, 1305, 1306, 1307, 1308, 1309,
                1310, 1311, 1312, 1313, 1314, 1315, 1316, 1317, 1318, 1319, 1320, 1321, 1322, 1323,
                1324, 1325, 1326, 1327, 1328, 1329, 1330, 1331, 1332, 1333, 1334, 1335, 1336, 1337,
                1338, 1339, 1340, 1341, 1342, 1343, 1344, 1345, 1346, 1347, 1348, 1349, 1350, 1351,
                1352, 1353, 1354, 1355, 1356, 1357, 1358, 1359, 1360, 1361, 1362, 1363, 1364, 1365,
                1366, 1367, 1368, 1369, 1370, 1371, 1372, 1373, 1374, 1375, 1376, 1377, 1378, 1379,
                1380, 1381, 1382, 1383, 1384, 1385, 1386, 1387, 1388, 1389, 1390, 1391, 1392, 1393,
                1394, 1395, 1396, 1397, 1398, 1399, 1400, 1401, 1402, 1403, 1404, 1405, 1406, 1407,
                1408, 1409, 1410, 1411, 1412, 1413, 1414, 1415, 1416, 1417, 1418, 1419, 1420, 1421,
                1422, 1423, 1424, 1425, 1426, 1427, 1428, 1429, 1430, 1431, 1432, 1433, 1434, 1435,
                1436, 1437, 1438, 1439, 1440, 1441, 1442, 1443, 1444, 1445, 1446, 1447, 1448, 1449,
                1450, 1451, 1452, 1453, 1454, 1455, 1456, 1457, 1458, 1459, 1460, 1461, 1462, 1463,
                1464, 1465, 1466, 1467, 1468, 1469, 1470, 1471, 1472, 1473, 1474, 1475, 1476, 1477,
                1478, 1479, 1480, 1481, 1482, 1483, 1484, 1485, 1486, 1487, 1488, 1489, 1490, 1491,
                1492, 1493, 1494, 1495, 1496, 1497, 1498, 1499, 1500, 1501, 1502, 1503, 1504, 1505,
                1506, 1507, 1508, 1509, 1510, 1511, 1512, 1513, 1514, 1515, 1516, 1517, 1518, 1519,
                1520, 1521, 1522, 1523, 1524, 1525, 1526, 1527, 1528, 1529, 1530, 1531, 1532, 1533,
                1534, 1535, 1536, 1537, 1538, 1539, 1540, 1541, 1542, 1543, 1544, 1545, 1546, 1547,
                1548, 1549, 1550, 1551, 1552, 1553, 1554, 1555, 1556, 1557, 1558, 1559, 1560, 1561,
                1562, 1563, 1564, 1565, 1566, 1567, 1568, 1569, 1570, 1571, 1572, 1573, 1574, 1575,
                1576, 1577, 1578, 1579, 1580, 1581, 1582, 1583, 1584, 1585, 1586, 1587, 1588, 1589,
                1590, 1591, 1592, 1593, 1594, 1595, 1596, 1597, 1598, 1599, 1600, 1601, 1602, 1603,
                1604, 1605, 1606, 1607, 1608, 1609, 1610, 1611, 1612, 1613, 1614, 1615, 1616, 1617,
                1618, 1619, 1620, 1621, 1622, 1623, 1624, 1625, 1626, 1627, 1628, 1629, 1630, 1631,
                1632, 1633, 1634, 1635, 1636, 1637, 1638, 1639, 1640, 1641, 1642, 1643, 1644, 1645,
                1646, 1647, 1648, 1649, 1650, 1651, 1652, 1653, 1654, 1655, 1656, 1657, 1658, 1659,
                1660, 1661, 1662, 1663, 1664, 1665, 1666, 1667, 1668, 1669, 1670, 1671, 1672, 1673,
                1674, 1675, 1676, 1677, 1678, 1679, 1680, 1681, 1682, 1683, 1684, 1685, 1686, 1687,
                1688, 1689, 1690, 1691, 1692, 1693, 1694, 1695, 1696, 1697, 1698, 1699, 1700, 1701,
                1702, 1703, 1704, 1705, 1706, 1707, 1708, 1709, 1710, 1711, 1712, 1713, 1714, 1715,
                1716, 1717, 1718, 1719, 1720, 1721, 1722, 1723, 1724, 1725, 1726, 1727, 1728, 1729,
                1730, 1731, 1732, 1733, 1734, 1735, 1736, 1737, 1738, 1739, 1740, 1741, 1742, 1743,
                1744, 1745, 1746, 1747, 1748, 1749, 1750, 1751, 1752, 1753, 1754, 1755, 1756, 1757,
                1758, 1759, 1760, 1761, 1762, 1763, 1764, 1765, 1766, 1767, 1768, 1769, 1770, 1771,
                1772, 1773, 1774, 1775, 1776, 1777, 1778, 1779, 1780, 1781, 1782, 1783, 1784, 1785,
                1786, 1787, 1788, 1789, 1790, 1791, 1792, 1793, 1794, 1795, 1796, 1797, 1798, 1799,
                1800, 1801, 1802, 1803, 1804, 1805, 1806, 1807, 1808, 1809, 1810, 1811, 1812, 1813,
                1814, 1815, 1816, 1817, 1818, 1819, 1820, 1821, 1822, 1823, 1824, 1825, 1826, 1827,
                1828, 1829, 1830, 1831, 1832, 1833, 1834, 1835, 1836, 1837, 1838, 1839, 1840, 1841,
                1842, 1843, 1844, 1845, 1846, 1847, 1848, 1849, 1850, 1851, 1852, 1853, 1854, 1855,
                1856, 1857, 1858, 1859, 1860, 1861, 1862, 1863, 1864, 1865, 1866, 1867, 1868, 1869,
                1870, 1871, 1872, 1873, 1874, 1875, 1876, 1877, 1878, 1879, 1880, 1881, 1882, 1883,
                1884, 1885, 1886, 1887, 1888, 1889, 1890, 1891, 1892, 1893, 1894, 1895, 1896, 1897,
                1898, 1899, 1900, 1901, 1902, 1903, 1904, 1905, 1906, 1907, 1908, 1909, 1910, 1911,
                1912, 1913, 1914, 1915, 1916, 1917, 1918, 1919, 1920, 1921, 1922, 1923, 1924, 1925,
                1926, 1927, 1928, 1929, 1930, 1931, 1932, 1933, 1934, 1935, 1936, 1937, 1938, 1939,
                1940, 1941, 1942, 1943, 1944, 1945, 1946, 1947, 1948, 1949, 1950, 1951, 1952, 1953,
                1954, 1955, 1956, 1957, 1958, 1959, 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967,
                1968, 1969, 1970, 1971, 1972, 1973, 1974, 1975, 1976, 1977, 1978, 1979, 1980, 1981,
                1982, 1983, 1984, 1985, 1986, 1987, 1988, 1989, 1990, 1991, 1992, 1993, 1994, 1995,
                1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009,
                2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023,
                2024, 2025, 2026, 2027, 2028, 2029, 2030, 2031, 2032, 2033, 2034, 2035, 2036, 2037,
                2038, 2039, 2040, 2041, 2042, 2043, 2044, 2045, 2046, 2047, 2048, 2049, 2050, 2051,
                2052, 2053, 2054, 2055, 2056, 2057, 2058, 2059, 2060, 2061, 2062, 2063, 2064, 2065,
                2066, 2067, 2068, 2069, 2070, 2071, 2072, 2073, 2074, 2075, 2076, 2077, 2078, 2079,
                2080, 2081, 2082, 2083, 2084, 2085, 2086, 2087, 2088, 2089, 2090, 2091, 2092, 2093,
                2094, 2095, 2096, 2097, 2098, 2099, 2100, 2101, 2102, 2103, 2104, 2105, 2106, 2107,
                2108, 2109, 2110, 2111, 2112, 2113, 2114, 2115, 2116, 2117, 2118, 2119, 2120, 2121,
                2122, 2123, 2124, 2125, 2126, 2127, 2128, 2129, 2130, 2131, 2132, 2133, 2134, 2135,
                2136, 2137, 2138, 2139, 2140, 2141, 2142, 2143, 2144, 2145, 2146, 2147, 2148, 2149,
                2150, 2151, 2152, 2153, 2154, 2155, 2156, 2157, 2158, 2159, 2160, 2161, 2162, 2163,
                2164, 2165, 2166, 2167, 2168, 2169, 2170, 2171, 2172, 2173, 2174, 2175, 2176, 2177,
                2178, 2179, 2180, 2181, 2182, 2183, 2184, 2185, 2186, 2187, 2188, 2189, 2190, 2191,
                2192, 2193, 2194, 2195, 2196, 2197, 2198, 2199, 2200, 2201, 2202, 2203, 2204, 2205,
                2206, 2207, 2208, 2209, 2210, 2211, 2212, 2213, 2214, 2215, 2216, 2217, 2218, 2219,
                2220, 2221, 2222, 2223, 2224, 2225, 2226, 2227, 2228, 2229, 2230, 2231, 2232, 2233,
                2234, 2235, 2236, 2237, 2238, 2239, 2240, 2241, 2242, 2243, 2244, 2245, 2246, 2247,
                2248, 2249, 2250, 2251, 2252, 2253, 2254, 2255, 2256, 2257, 2258, 2259, 2260, 2261,
                2262, 2263, 2264, 2265, 2266, 2267, 2268, 2269, 2270, 2271, 2272, 2273, 2274, 2275,
                2276, 2277, 2278, 2279, 2280, 2281, 2282, 2283, 2284, 2285, 2286, 2287, 2288, 2289,
                2290, 2291, 2292, 2293, 2294, 2295, 2296, 2297, 2298, 2299, 2300, 2301, 2302, 2303,
                2304, 2305, 2306, 2307, 2308, 2309, 2310, 2311, 2312, 2313, 2314, 2315, 2316, 2317,
                2318, 2319, 2320, 2321, 2322, 2323, 2324, 2325, 2326, 2327, 2328, 2329, 2330, 2331,
                2332, 2333, 2334, 2335, 2336, 2337, 2338, 2339, 2340, 2341, 2342, 2343, 2344, 2345,
                2346, 2347, 2348, 2349, 2350, 2351, 2352, 2353, 2354, 2355, 2356, 2357, 2358, 2359,
                2360, 2361, 2362, 2363, 2364, 2365, 2366, 2367, 2368, 2369, 2370, 2371, 2372, 2373,
                2374, 2375, 2376, 2377, 2378, 2379, 2380, 2381, 2382, 2383, 2384, 2385, 2386, 2387,
                2388, 2389, 2390, 2391, 2392, 2393, 2394, 2395, 2396, 2397, 2398, 2399, 2400, 2401,
                2402, 2403, 2404, 2405, 2406, 2407, 2408, 2409, 2410, 2411, 2412, 2413, 2414, 2415,
                2416, 2417, 2418, 2419, 2420, 2421, 2422, 2423, 2424, 2425, 2426, 2427, 2428, 2429,
                2430, 2431, 2432, 2433, 2434, 2435, 2436, 2437, 2438, 2439, 2440, 2441, 2442, 2443,
                2444, 2445, 2446, 2447, 2448, 2449, 2450, 2451, 2452, 2453, 2454, 2455, 2456, 2457,
                2458, 2459, 2460, 2461, 2462, 2463, 2464, 2465, 2466, 2467, 2468, 2469, 2470, 2471,
                2472, 2473, 2474, 2475, 2476, 2477, 2478, 2479, 2480, 2481, 2482, 2483, 2484, 2485,
                2486, 2487, 2488, 2489, 2490, 2491, 2492, 2493, 2494, 2495, 2496, 2497, 2498, 2499,
                2500
            ]
        );
    }

    #[test]
    fn test_negative_elements() {
        assert_eq!(longest_increasing_subsequence(vec![-2, -1]), vec![-2, -1]);
    }
}
}

最大正方形

#![allow(unused)]
fn main() {
use std::cmp::max;
use std::cmp::min;

/// Maximal Square
/// Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.
/// https://leetcode.com/problems/maximal-square/
///
/// Arguments:
///     * `matrix` - an array of integer array
/// Complexity
///     - time complexity: O(n^2),
///     - space complexity: O(n),
pub fn maximal_square(matrix: &mut Vec<Vec<i32>>) -> i32 {
    if matrix.is_empty() {
        return 0;
    }

    let rows = matrix.len();
    let cols = matrix[0].len();
    let mut result: i32 = 0;

    for row in 0..rows {
        for col in 0..cols {
            if matrix[row][col] == 1 {
                if row == 0 || col == 0 {
                    result = max(result, 1);
                } else {
                    let temp = min(matrix[row - 1][col - 1], matrix[row - 1][col]);

                    let count: i32 = min(temp, matrix[row][col - 1]) + 1;
                    result = max(result, count);

                    matrix[row][col] = count;
                }
            }
        }
    }

    result * result
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test() {
        assert_eq!(maximal_square(&mut vec![]), 0);

        let mut matrix = vec![vec![0, 1], vec![1, 0]];
        assert_eq!(maximal_square(&mut matrix), 1);

        let mut matrix = vec![
            vec![1, 0, 1, 0, 0],
            vec![1, 0, 1, 1, 1],
            vec![1, 1, 1, 1, 1],
            vec![1, 0, 0, 1, 0],
        ];
        assert_eq!(maximal_square(&mut matrix), 4);

        let mut matrix = vec![vec![0]];
        assert_eq!(maximal_square(&mut matrix), 0);
    }
}
}

最大子数组

#![allow(unused)]
fn main() {
/// ## maximum subarray via Dynamic Programming

/// maximum_subarray(array) find the subarray (containing at least one number) which has the largest sum
/// and return its sum.
///
/// A subarray is a contiguous part of an array.
///
/// Arguments:
///     * `array` - an integer array
/// Complexity
///     - time complexity: O(array.length),
///     - space complexity: O(array.length),
pub fn maximum_subarray(array: &[i32]) -> i32 {
    let mut dp = vec![0; array.len()];
    dp[0] = array[0];
    let mut result = dp[0];

    for i in 1..array.len() {
        if dp[i - 1] > 0 {
            dp[i] = dp[i - 1] + array[i];
        } else {
            dp[i] = array[i];
        }
        result = result.max(dp[i]);
    }

    result
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn non_negative() {
        //the maximum value: 1 + 0 + 5 + 8 = 14
        let array = vec![1, 0, 5, 8];
        assert_eq!(maximum_subarray(&array), 14);
    }

    #[test]
    fn negative() {
        //the maximum value: -1
        let array = vec![-3, -1, -8, -2];
        assert_eq!(maximum_subarray(&array), -1);
    }

    #[test]
    fn normal() {
        //the maximum value: 3 + (-2) + 5 = 6
        let array = vec![-4, 3, -2, 5, -8];
        assert_eq!(maximum_subarray(&array), 6);
    }

    #[test]
    fn single_element() {
        let array = vec![6];
        assert_eq!(maximum_subarray(&array), 6);
        let array = vec![-6];
        assert_eq!(maximum_subarray(&array), -6);
    }
}
}

棒的切割

#![allow(unused)]
fn main() {
//! Solves the rod-cutting problem
use std::cmp::max;

/// `rod_cut(p)` returns the maximum possible profit if a rod of length `n` = `p.len()`
/// is cut into up to `n` pieces, where the profit gained from each piece of length
/// `l` is determined by `p[l - 1]` and the total profit is the sum of the profit
/// gained from each piece.
///
/// # Arguments
///    - `p` - profit for rods of length 1 to n inclusive
///
/// # Complexity
///    - time complexity: O(n^2),
///    - space complexity: O(n^2),
///
/// where n is the length of `p`.
pub fn rod_cut(p: &[usize]) -> usize {
    let n = p.len();
    // f is the dynamic programming table
    let mut f = vec![0; n];

    for i in 0..n {
        let mut max_price = p[i];
        for j in 1..=i {
            max_price = max(max_price, p[j - 1] + f[i - j]);
        }
        f[i] = max_price;
    }

    // accomodate for input with length zero
    if n != 0 {
        f[n - 1]
    } else {
        0
    }
}

#[cfg(test)]
mod tests {
    use super::rod_cut;

    #[test]
    fn test_rod_cut() {
        assert_eq!(0, rod_cut(&[]));
        assert_eq!(15, rod_cut(&[5, 8, 2]));
        assert_eq!(10, rod_cut(&[1, 5, 8, 9]));
        assert_eq!(25, rod_cut(&[5, 8, 2, 1, 7]));
        assert_eq!(87, rod_cut(&[0, 0, 0, 0, 0, 87]));
        assert_eq!(49, rod_cut(&[7, 6, 5, 4, 3, 2, 1]));
        assert_eq!(22, rod_cut(&[1, 5, 8, 9, 10, 17, 17, 20]));
        assert_eq!(60, rod_cut(&[6, 4, 8, 2, 5, 8, 2, 3, 7, 11]));
        assert_eq!(30, rod_cut(&[1, 5, 8, 9, 10, 17, 17, 20, 24, 30]));
        assert_eq!(12, rod_cut(&[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]));
    }
}
}

扩展欧几里得算法

#![allow(unused)]
fn main() {
fn update_step(a: &mut i32, old_a: &mut i32, quotient: i32) {
    let temp = *a;
    *a = *old_a - quotient * temp;
    *old_a = temp;
}

pub fn extended_euclidean_algorithm(a: i32, b: i32) -> (i32, i32, i32) {
    let (mut old_r, mut rem) = (a, b);
    let (mut old_s, mut coeff_s) = (1, 0);
    let (mut old_t, mut coeff_t) = (0, 1);

    while rem != 0 {
        let quotient = old_r / rem;

        update_step(&mut rem, &mut old_r, quotient);
        update_step(&mut coeff_s, &mut old_s, quotient);
        update_step(&mut coeff_t, &mut old_t, quotient);
    }

    (old_r, old_s, old_t)
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        assert_eq!(extended_euclidean_algorithm(101, 13), (1, 4, -31));
        assert_eq!(extended_euclidean_algorithm(123, 19), (1, -2, 13));
        assert_eq!(extended_euclidean_algorithm(25, 36), (1, 13, -9));
        assert_eq!(extended_euclidean_algorithm(69, 54), (3, -7, 9));
        assert_eq!(extended_euclidean_algorithm(55, 79), (1, 23, -16));
        assert_eq!(extended_euclidean_algorithm(33, 44), (11, -1, 1));
        assert_eq!(extended_euclidean_algorithm(50, 70), (10, 3, -2));
    }
}
}

最大公约数

#![allow(unused)]
fn main() {
/// Greatest Common Divisor.
///
/// greatest_common_divisor(num1, num2) returns the greatest number of num1 and num2.
///
/// Wikipedia reference: https://en.wikipedia.org/wiki/Greatest_common_divisor
/// gcd(a, b) = gcd(a, -b) = gcd(-a, b) = gcd(-a, -b) by definition of divisibility

pub fn greatest_common_divisor_recursive(a: i64, b: i64) -> i64 {
    if a == 0 {
        b.abs()
    } else {
        greatest_common_divisor_recursive(b % a, a)
    }
}

pub fn greatest_common_divisor_iterative(mut a: i64, mut b: i64) -> i64 {
    while a != 0 {
        let remainder = b % a;
        b = a;
        a = remainder;
    }
    b.abs()
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn positive_number_recursive() {
        assert_eq!(greatest_common_divisor_recursive(4, 16), 4);
        assert_eq!(greatest_common_divisor_recursive(16, 4), 4);
        assert_eq!(greatest_common_divisor_recursive(3, 5), 1);
        assert_eq!(greatest_common_divisor_recursive(40, 40), 40);
        assert_eq!(greatest_common_divisor_recursive(27, 12), 3);
    }

    #[test]
    fn positive_number_iterative() {
        assert_eq!(greatest_common_divisor_iterative(4, 16), 4);
        assert_eq!(greatest_common_divisor_iterative(16, 4), 4);
        assert_eq!(greatest_common_divisor_iterative(3, 5), 1);
        assert_eq!(greatest_common_divisor_iterative(40, 40), 40);
        assert_eq!(greatest_common_divisor_iterative(27, 12), 3);
    }

    #[test]
    fn negative_number_recursive() {
        assert_eq!(greatest_common_divisor_recursive(-32, -8), 8);
        assert_eq!(greatest_common_divisor_recursive(-8, -32), 8);
        assert_eq!(greatest_common_divisor_recursive(-3, -5), 1);
        assert_eq!(greatest_common_divisor_recursive(-40, -40), 40);
        assert_eq!(greatest_common_divisor_recursive(-12, -27), 3);
    }

    #[test]
    fn negative_number_iterative() {
        assert_eq!(greatest_common_divisor_iterative(-32, -8), 8);
        assert_eq!(greatest_common_divisor_iterative(-8, -32), 8);
        assert_eq!(greatest_common_divisor_iterative(-3, -5), 1);
        assert_eq!(greatest_common_divisor_iterative(-40, -40), 40);
        assert_eq!(greatest_common_divisor_iterative(-12, -27), 3);
    }

    #[test]
    fn mix_recursive() {
        assert_eq!(greatest_common_divisor_recursive(0, -5), 5);
        assert_eq!(greatest_common_divisor_recursive(-5, 0), 5);
        assert_eq!(greatest_common_divisor_recursive(-64, 32), 32);
        assert_eq!(greatest_common_divisor_recursive(-32, 64), 32);
        assert_eq!(greatest_common_divisor_recursive(-40, 40), 40);
        assert_eq!(greatest_common_divisor_recursive(12, -27), 3);
    }

    #[test]
    fn mix_iterative() {
        assert_eq!(greatest_common_divisor_iterative(0, -5), 5);
        assert_eq!(greatest_common_divisor_iterative(-5, 0), 5);
        assert_eq!(greatest_common_divisor_iterative(-64, 32), 32);
        assert_eq!(greatest_common_divisor_iterative(-32, 64), 32);
        assert_eq!(greatest_common_divisor_iterative(-40, 40), 40);
        assert_eq!(greatest_common_divisor_iterative(12, -27), 3);
    }
}
}

帕斯卡三角

#![allow(unused)]
fn main() {
/// ## Paslcal's triangle problem

/// pascal_triangle(num_rows) returns the first num_rows of Pascal's triangle.
/// About Pascal's triangle: https://en.wikipedia.org/wiki/Pascal%27s_triangle
///
/// Arguments:
///     * `num_rows` - number of rows of triangle
/// Complexity
///     - time complexity: O(n^2),
///     - space complexity: O(n^2),
pub fn pascal_triangle(num_rows: i32) -> Vec<Vec<i32>> {
    let mut ans: Vec<Vec<i32>> = vec![];

    for i in 1..num_rows + 1 {
        let mut vec: Vec<i32> = vec![1];

        let mut res: i32 = 1;
        for k in 1..i {
            res *= i - k;
            res /= k;
            vec.push(res);
        }
        ans.push(vec);
    }

    ans
}

#[cfg(test)]
mod tests {
    use super::pascal_triangle;

    #[test]
    fn test() {
        assert_eq!(pascal_triangle(3), vec![vec![1], vec![1, 1], vec![1, 2, 1]]);
        assert_eq!(
            pascal_triangle(4),
            vec![vec![1], vec![1, 1], vec![1, 2, 1], vec![1, 3, 3, 1]]
        );
        assert_eq!(
            pascal_triangle(5),
            vec![
                vec![1],
                vec![1, 1],
                vec![1, 2, 1],
                vec![1, 3, 3, 1],
                vec![1, 4, 6, 4, 1]
            ]
        );
    }
}
}

寻找完美数

#![allow(unused)]
fn main() {
pub fn is_perfect_number(num: usize) -> bool {
    let mut sum = 0;

    for i in 1..num - 1 {
        if num % i == 0 {
            sum += i;
        }
    }

    num == sum
}

pub fn perfect_numbers(max: usize) -> Vec<usize> {
    let mut result: Vec<usize> = Vec::new();

    // It is not known if there are any odd perfect numbers, so we go around all the numbers.
    for i in 1..max + 1 {
        if is_perfect_number(i) {
            result.push(i);
        }
    }

    result
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        assert_eq!(is_perfect_number(6), true);
        assert_eq!(is_perfect_number(28), true);
        assert_eq!(is_perfect_number(496), true);
        assert_eq!(is_perfect_number(8128), true);

        assert_eq!(is_perfect_number(5), false);
        assert_eq!(is_perfect_number(86), false);
        assert_eq!(is_perfect_number(497), false);
        assert_eq!(is_perfect_number(8120), false);

        assert_eq!(perfect_numbers(10), vec![6]);
        assert_eq!(perfect_numbers(100), vec![6, 28]);
        assert_eq!(perfect_numbers(496), vec![6, 28, 496]);
        assert_eq!(perfect_numbers(1000), vec![6, 28, 496]);
    }
}
}

质数检测

#![allow(unused)]
fn main() {
pub fn prime_check(num: usize) -> bool {
    if (num > 1) & (num < 4) {
        return true;
    } else if (num < 2) || (num % 2 == 0) {
        return false;
    }

    let stop: usize = (num as f64).sqrt() as usize + 1;
    for i in (3..stop).step_by(2) {
        if num % i == 0 {
            return false;
        }
    }
    true
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        assert_eq!(prime_check(3), true);
        assert_eq!(prime_check(7), true);
        assert_eq!(prime_check(11), true);
        assert_eq!(prime_check(2003), true);

        assert_eq!(prime_check(4), false);
        assert_eq!(prime_check(6), false);
        assert_eq!(prime_check(21), false);
        assert_eq!(prime_check(2004), false);
    }
}
}

质数筛法

#![allow(unused)]
fn main() {
pub fn prime_numbers(max: usize) -> Vec<usize> {
    let mut result: Vec<usize> = Vec::new();

    if max >= 2 {
        result.push(2)
    }
    for i in (3..max + 1).step_by(2) {
        let stop: usize = (i as f64).sqrt() as usize + 1;
        let mut status: bool = true;

        for j in (3..stop).step_by(2) {
            if i % j == 0 {
                status = false
            }
        }
        if status {
            result.push(i)
        }
    }

    result
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        assert_eq!(prime_numbers(0), vec![]);
        assert_eq!(prime_numbers(11), vec![2, 3, 5, 7, 11]);
        assert_eq!(prime_numbers(25), vec![2, 3, 5, 7, 11, 13, 17, 19, 23]);
        assert_eq!(
            prime_numbers(33),
            vec![2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]
        );
    }
}
}

试除法

#![allow(unused)]
fn main() {
fn floor(value: f64, scale: u8) -> f64 {
    let multiplier = 10i64.pow(scale as u32) as f64;
    (value * multiplier).floor()
}

fn double_to_int(amount: f64) -> i128 {
    amount.round() as i128
}

pub fn trial_division(mut num: i128) -> Vec<i128> {
    let mut result: Vec<i128> = vec![];

    while num % 2 == 0 {
        result.push(2);
        num /= 2;
        num = double_to_int(floor(num as f64, 0))
    }
    let mut f: i128 = 3;

    while f.pow(2) <= num {
        if num % f == 0 {
            result.push(f);
            num /= f;
            num = double_to_int(floor(num as f64, 0))
        } else {
            f += 2
        }
    }

    if num != 1 {
        result.push(num)
    }
    result
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn basic() {
        assert_eq!(trial_division(9), vec!(3, 3));
        assert_eq!(trial_division(10), vec!(2, 5));
        assert_eq!(trial_division(11), vec!(11));
        assert_eq!(trial_division(33), vec!(3, 11));
        assert_eq!(trial_division(2003), vec!(2003));
        assert_eq!(trial_division(100001), vec!(11, 9091));
    }
}
}

最近点算法

#![allow(unused)]
fn main() {
type Point = (f64, f64);
use std::cmp::Ordering;

fn point_cmp((a1, a2): &Point, (b1, b2): &Point) -> Ordering {
    let acmp = f64_cmp(a1, b1);
    match acmp {
        Ordering::Equal => f64_cmp(a2, b2),
        _ => acmp,
    }
}

fn f64_cmp(a: &f64, b: &f64) -> Ordering {
    a.partial_cmp(b).unwrap()
}

/// returns the two closest points
/// or None if there are zero or one point
pub fn closest_points(points: &[Point]) -> Option<(Point, Point)> {
    let mut points: Vec<Point> = points.to_vec();
    points.sort_by(point_cmp);

    closest_points_aux(&points, 0, points.len())
}

fn dist((x1, y1): &Point, (x2, y2): &Point) -> f64 {
    let dx = *x1 - *x2;
    let dy = *y1 - *y2;

    (dx * dx + dy * dy).sqrt()
}

fn closest_points_aux(
    points: &[Point],
    mut start: usize,
    mut end: usize,
) -> Option<(Point, Point)> {
    let n = end - start;

    if n <= 1 {
        return None;
    }

    if n <= 3 {
        // bruteforce
        let mut min = dist(&points[0], &points[1]);
        let mut pair = (points[0], points[1]);

        for i in 0..n {
            for j in (i + 1)..n {
                let new = dist(&points[i], &points[j]);
                if new < min {
                    min = new;
                    pair = (points[i], points[j]);
                }
            }
        }
        return Some(pair);
    }

    let mid = (start + end) / 2;
    let left = closest_points_aux(points, start, mid);
    let right = closest_points_aux(points, mid, end);

    let (mut min_dist, mut pair) = match (left, right) {
        (Some((l1, l2)), Some((r1, r2))) => {
            let dl = dist(&l1, &l2);
            let dr = dist(&r1, &r2);
            if dl < dr {
                (dl, (l1, l2))
            } else {
                (dr, (r1, r2))
            }
        }
        (Some((a, b)), None) => (dist(&a, &b), (a, b)),
        (None, Some((a, b))) => (dist(&a, &b), (a, b)),
        (None, None) => unreachable!(),
    };

    let mid_x = points[mid].0;
    while points[start].0 < mid_x - min_dist {
        start += 1;
    }
    while points[end - 1].0 > mid_x + min_dist {
        end -= 1;
    }

    let mut mids: Vec<&Point> = points[start..end].iter().collect();
    mids.sort_by(|a, b| f64_cmp(&a.1, &b.1));

    for (i, e) in mids.iter().enumerate() {
        for k in 1..8 {
            if i + k >= mids.len() {
                break;
            }

            let new = dist(e, mids[i + k]);
            if new < min_dist {
                min_dist = new;
                pair = (**e, *mids[i + k]);
            }
        }
    }

    Some(pair)
}

#[cfg(test)]
mod tests {
    use super::closest_points;
    use super::Point;

    fn eq(p1: Option<(Point, Point)>, p2: Option<(Point, Point)>) -> bool {
        match (p1, p2) {
            (None, None) => true,
            (Some((p1, p2)), Some((p3, p4))) => (p1 == p3 && p2 == p4) || (p1 == p4 && p2 == p3),
            _ => false,
        }
    }

    macro_rules! assert_display {
        ($left: expr, $right: expr) => {
            assert!(
                eq($left, $right),
                "assertion failed: `(left == right)`\nleft: `{:?}`,\nright: `{:?}`",
                $left,
                $right
            )
        };
    }

    #[test]
    fn zero_points() {
        let vals: [Point; 0] = [];
        assert_display!(closest_points(&vals), None::<(Point, Point)>);
    }

    #[test]
    fn one_points() {
        let vals = [(0., 0.)];
        assert_display!(closest_points(&vals), None::<(Point, Point)>);
    }

    #[test]
    fn two_points() {
        let vals = [(0., 0.), (1., 1.)];
        assert_display!(closest_points(&vals), Some(((0., 0.), (1., 1.))));
    }

    #[test]
    fn three_points() {
        let vals = [(0., 0.), (1., 1.), (3., 3.)];
        assert_display!(closest_points(&vals), Some(((0., 0.), (1., 1.))));
    }

    #[test]
    fn list_1() {
        let vals = [
            (0., 0.),
            (2., 1.),
            (5., 2.),
            (2., 3.),
            (4., 0.),
            (0., 4.),
            (5., 6.),
            (4., 4.),
            (7., 3.),
            (-1., 2.),
            (2., 6.),
        ];
        assert_display!(closest_points(&vals), Some(((2., 1.), (2., 3.))));
    }

    #[test]
    fn list_2() {
        let vals = [
            (1., 3.),
            (4., 6.),
            (8., 8.),
            (7., 5.),
            (5., 3.),
            (10., 3.),
            (7., 1.),
            (8., 3.),
            (4., 9.),
            (4., 12.),
            (4., 15.),
            (7., 14.),
            (8., 12.),
            (6., 10.),
            (4., 14.),
            (2., 7.),
            (3., 8.),
            (5., 8.),
            (6., 7.),
            (8., 10.),
            (6., 12.),
        ];
        assert_display!(closest_points(&vals), Some(((4., 14.), (4., 15.))));
    }

    #[test]
    fn vertical_points() {
        let vals = [
            (0., 0.),
            (0., 50.),
            (0., -25.),
            (0., 40.),
            (0., 42.),
            (0., 100.),
            (0., 17.),
            (0., 29.),
            (0., -50.),
            (0., 37.),
            (0., 34.),
            (0., 8.),
            (0., 3.),
            (0., 46.),
        ];
        assert_display!(closest_points(&vals), Some(((0., 40.), (0., 42.))));
    }
}
}

加密算法

数据加密的基本过程就是对原来为明文的文件或数据按某种算法进行处理，使其成为不可读的一段代码为“密文”，使其只能在输入相应的密钥之后才能显示出原容，通过这样的途径来达到保护数据不被非法人窃取、阅读的目的。 该过程的逆过程为解密，即将该编码信息转化为其原来数据的过程。

随着信息化和数字化社会的发展，人们对信息安全和保密的重要性认识不断提高，于是在1997年，美国国家标准局公布实施了“美国数据加密标准（DES）”，民间力量开始全面介入密码学的研究和应用中，采用的加密算法有DES、RSA、SHA等。随着对加密强度需求的不断提高，近期又出现了AES、ECC等。 使用密码学可以达到以下目的：

• 保密性：防止用户的标识或数据被读取。
• 数据完整性：防止数据被更改。
• 身份验证：确保数据发自特定的一方。

凯撒算法(caesar)

#![allow(unused)]
fn main() {
pub fn another_rot13(text: &str) -> String {
    let input = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz";
    let output = "NOPQRSTUVWXYZABCDEFGHIJKLMnopqrstuvwxyzabcdefghijklm";
    text.chars()
        .map(|c| match input.find(c) {
            Some(i) => output.chars().nth(i).unwrap(),
            None => c,
        })
        .collect()
}

#[cfg(test)]
mod tests {
    // Note this useful idiom: importing names from outer (for mod tests) scope.
    use super::*;

    #[test]
    fn test_simple() {
        assert_eq!(another_rot13("ABCzyx"), "NOPmlk");
    }

    #[test]
    fn test_every_alphabet_with_space() {
        assert_eq!(
            another_rot13("The quick brown fox jumps over the lazy dog"),
            "Gur dhvpx oebja sbk whzcf bire gur ynml qbt"
        );
    }

    #[test]
    fn test_non_alphabet() {
        assert_eq!(another_rot13("🎃 Jack-o'-lantern"), "🎃 Wnpx-b'-ynagrea");
    }
}
}

摩斯码

#![allow(unused)]
fn main() {
use std::collections::HashMap;
use std::io;

const UNKNOWN_CHARACTER: &str = "........";
const _UNKNOWN_MORSE_CHARACTER: &str = "_";

pub fn encode(message: &str) -> String {
    let dictionary = _morse_dictionary();
    message
        .chars()
        .into_iter()
        .map(|char| char.to_uppercase().to_string())
        .map(|letter| dictionary.get(letter.as_str()))
        .map(|option| option.unwrap_or(&UNKNOWN_CHARACTER).to_string())
        .collect::<Vec<String>>()
        .join(" ")
}

// Declaritive macro for creating readable map declarations, for more info see https://doc.rust-lang.org/book/ch19-06-macros.html
macro_rules! map {
    ($($key:expr => $value:expr),* $(,)?) => {
        std::iter::Iterator::collect(std::array::IntoIter::new([$(($key, $value),)*]))
    };
}

fn _morse_dictionary() -> HashMap<&'static str, &'static str> {
    map! {
        "A" => ".-",      "B" => "-...",    "C" => "-.-.",
        "D" => "-..",     "E" => ".",       "F" => "..-.",
        "G" => "--.",     "H" => "....",    "I" => "..",
        "J" => ".---",    "K" => "-.-",     "L" => ".-..",
        "M" => "--",      "N" => "-.",      "O" => "---",
        "P" => ".--.",    "Q" => "--.-",    "R" => ".-.",
        "S" => "...",     "T" => "-",       "U" => "..-",
        "V" => "...-",    "W" => ".--",     "X" => "-..-",
        "Y" => "-.--",    "Z" => "--..",

        "1" => ".----",   "2" => "..---",   "3" => "...--",
        "4" => "....-",   "5" => ".....",   "6" => "-....",
        "7" => "--...",   "8" => "---..",   "9" => "----.",
        "0" => "-----",

        "&" => ".-...",   "@" => ".--.-.",  ":" => "---...",
        "," => "--..--",  "." => ".-.-.-",  "'" => ".----.",
        "\"" => ".-..-.", "?" => "..--..",  "/" => "-..-.",
        "=" => "-...-",   "+" => ".-.-.",   "-" => "-....-",
        "(" => "-.--.",   ")" => "-.--.-",  " " => "/",
        "!" => "-.-.--",
    }
}

fn _morse_to_alphanumeric_dictionary() -> HashMap<&'static str, &'static str> {
    map! {
        ".-"   =>  "A",      "-..." => "B",    "-.-." => "C",
        "-.."  =>  "D",      "."    => "E",       "..-." => "F",
        "--."  =>  "G",      "...." => "H",    ".." => "I",
        ".---" =>  "J",     "-.-" => "K",     ".-.." => "L",
        "--"   =>  "M",       "-." => "N",      "---" => "O",
        ".--." =>  "P",     "--.-" => "Q",    ".-." => "R",
        "..."  =>  "S",      "-" => "T",       "..-" => "U",
        "...-" =>  "V",     ".--" => "W",     "-..-" => "X",
        "-.--" =>  "Y",     "--.." => "Z",

        ".----" => "1",    "..---" => "2",   "...--" => "3",
        "....-" => "4",    "....." => "5",   "-...." => "6",
        "--..." => "7",    "---.." => "8",   "----." => "9",
        "-----" => "0",

        ".-..." => "&",    ".--.-." => "@",  "---..." => ":",
        "--..--" => ",",   ".-.-.-" => ".",  ".----." => "'",
        ".-..-." => "\"",  "..--.." => "?",  "-..-." => "/",
        "-...-" => "=",   ".-.-." => "+",   "-....-" => "-",
        "-.--." => "(",   "-.--.-" => ")",  "/" => " ",
        "-.-.--" => "!",  " " => " ",       "" => ""
    }
}

fn _check_part(string: &str) -> bool {
    for c in string.chars() {
        match c {
            '.' | '-' | ' ' => (),
            _ => return false,
        }
    }
    true
}

fn _check_all_parts(string: &str) -> bool {
    string.split('/').all(_check_part)
}

fn _decode_token(string: &str) -> String {
    _morse_to_alphanumeric_dictionary()
        .get(string)
        .unwrap_or(&_UNKNOWN_MORSE_CHARACTER)
        .to_string()
}

fn _decode_part(string: &str) -> String {
    string
        .split(' ')
        .map(_decode_token)
        .collect::<Vec<String>>()
        .join("")
}

/// Convert morse code to ascii.
///
/// Given a morse code, return the corresponding message.
/// If the code is invalid, the undecipherable part of the code is replaced by `_`.
pub fn decode(string: &str) -> Result<String, io::Error> {
    if !_check_all_parts(string) {
        return Err(io::Error::new(
            io::ErrorKind::InvalidData,
            "Invalid morse code",
        ));
    }

    let mut partitions: Vec<String> = vec![];

    for part in string.split('/') {
        partitions.push(_decode_part(part));
    }

    Ok(partitions.join(" "))
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn encrypt_only_letters() {
        let message = "Hello Morse";
        let cipher = encode(message);
        assert_eq!(
            cipher,
            ".... . .-.. .-.. --- / -- --- .-. ... .".to_string()
        )
    }

    #[test]
    fn encrypt_letters_and_special_characters() {
        let message = "What's a great day!";
        let cipher = encode(message);
        assert_eq!(
            cipher,
            ".-- .... .- - .----. ... / .- / --. .-. . .- - / -.. .- -.-- -.-.--".to_string()
        )
    }

    #[test]
    fn encrypt_message_with_unsupported_character() {
        let message = "Error?? {}";
        let cipher = encode(message);
        assert_eq!(
            cipher,
            ". .-. .-. --- .-. ..--.. ..--.. / ........ ........".to_string()
        )
    }

    #[test]
    fn decrypt_valid_morsecode_with_spaces() {
        let expected = "Hello Morse! How's it goin, \"eh\"?"
            .to_string()
            .to_uppercase();
        let encypted = encode(&expected);
        let result = decode(&encypted).unwrap();

        assert_eq!(expected, result);
    }

    #[test]
    fn decrypt_valid_character_set_invalid_morsecode() {
        let expected = format!(
            "{}{}{}{} {}",
            _UNKNOWN_MORSE_CHARACTER,
            _UNKNOWN_MORSE_CHARACTER,
            _UNKNOWN_MORSE_CHARACTER,
            _UNKNOWN_MORSE_CHARACTER,
            _UNKNOWN_MORSE_CHARACTER,
        );

        let encypted = ".-.-.--.-.-. --------. ..---.-.-. .-.-.--.-.-. / .-.-.--.-.-.".to_string();
        let result = decode(&encypted).unwrap();

        assert_eq!(expected, result);
    }

    #[test]
    fn decrypt_invalid_morsecode_with_spaces() {
        let encypted = "1... . .-.. .-.. --- / -- --- .-. ... .";
        let result = decode(encypted).map_err(|e| e.kind());
        let expected = Err(io::ErrorKind::InvalidData);

        assert_eq!(expected, result);
    }
}
}

Polibius密码

#![allow(unused)]
fn main() {
/// Encode an ASCII string into its location in a Polybius square.
/// Only alphabetical characters are encoded.
pub fn encode_ascii(string: &str) -> String {
    string
        .chars()
        .map(|c| match c {
            'a' | 'A' => "11",
            'b' | 'B' => "12",
            'c' | 'C' => "13",
            'd' | 'D' => "14",
            'e' | 'E' => "15",
            'f' | 'F' => "21",
            'g' | 'G' => "22",
            'h' | 'H' => "23",
            'i' | 'I' | 'j' | 'J' => "24",
            'k' | 'K' => "25",
            'l' | 'L' => "31",
            'm' | 'M' => "32",
            'n' | 'N' => "33",
            'o' | 'O' => "34",
            'p' | 'P' => "35",
            'q' | 'Q' => "41",
            'r' | 'R' => "42",
            's' | 'S' => "43",
            't' | 'T' => "44",
            'u' | 'U' => "45",
            'v' | 'V' => "51",
            'w' | 'W' => "52",
            'x' | 'X' => "53",
            'y' | 'Y' => "54",
            'z' | 'Z' => "55",
            _ => "",
        })
        .collect()
}

/// Decode a string of ints into their corresponding
/// letters in a Polybius square.
///
/// Any invalid characters, or whitespace will be ignored.
pub fn decode_ascii(string: &str) -> String {
    string
        .chars()
        .filter(|c| !c.is_whitespace())
        .collect::<String>()
        .as_bytes()
        .chunks(2)
        .map(|s| match std::str::from_utf8(s) {
            Ok(v) => v.parse::<i32>().unwrap_or(0),
            Err(_) => 0,
        })
        .map(|i| match i {
            11 => 'A',
            12 => 'B',
            13 => 'C',
            14 => 'D',
            15 => 'E',
            21 => 'F',
            22 => 'G',
            23 => 'H',
            24 => 'I',
            25 => 'K',
            31 => 'L',
            32 => 'M',
            33 => 'N',
            34 => 'O',
            35 => 'P',
            41 => 'Q',
            42 => 'R',
            43 => 'S',
            44 => 'T',
            45 => 'U',
            51 => 'V',
            52 => 'W',
            53 => 'X',
            54 => 'Y',
            55 => 'Z',
            _ => ' ',
        })
        .collect::<String>()
        .replace(" ", "")
}

#[cfg(test)]
mod tests {
    use super::{decode_ascii, encode_ascii};

    #[test]
    fn encode_empty() {
        assert_eq!(encode_ascii(""), "");
    }

    #[test]
    fn encode_valid_string() {
        assert_eq!(encode_ascii("This is a test"), "4423244324431144154344");
    }

    #[test]
    fn encode_emoji() {
        assert_eq!(encode_ascii("🙂"), "");
    }

    #[test]
    fn decode_empty() {
        assert_eq!(decode_ascii(""), "");
    }

    #[test]
    fn decode_valid_string() {
        assert_eq!(
            decode_ascii("44 23 24 43 24 43 11 44 15 43 44 "),
            "THISISATEST"
        );
    }

    #[test]
    fn decode_emoji() {
        assert_eq!(decode_ascii("🙂"), "");
    }

    #[test]
    fn decode_string_with_whitespace() {
        assert_eq!(
            decode_ascii("44\n23\t\r24\r\n43   2443\n 11 \t 44\r \r15 \n43 44"),
            "THISISATEST"
        );
    }

    #[test]
    fn decode_unknown_string() {
        assert_eq!(decode_ascii("94 63 64 83 64 48 77 00 05 47 48 "), "");
    }

    #[test]
    fn decode_odd_length() {
        assert_eq!(decode_ascii("11 22 33 4"), "AGN");
    }

    #[test]
    fn encode_and_decode() {
        let string = "Do you ever wonder why we're here?";
        let encode = encode_ascii(string);
        assert_eq!(
            "1434543445155115425234331415425223545215421523154215",
            encode,
        );
        assert_eq!("DOYOUEVERWONDERWHYWEREHERE", decode_ascii(&encode));
    }
}
}

rot13加密算法

#![allow(unused)]
fn main() {
pub fn rot13(text: &str) -> String {
    let to_enc = text.to_uppercase();
    to_enc
        .chars()
        .map(|c| match c {
            'A'..='M' => ((c as u8) + 13) as char,
            'N'..='Z' => ((c as u8) - 13) as char,
            _ => c,
        })
        .collect()
}

#[cfg(test)]
mod test {
    use super::*;

    #[test]
    fn test_single_letter() {
        assert_eq!("N", rot13("A"));
    }

    #[test]
    fn test_bunch_of_letters() {
        assert_eq!("NOP", rot13("ABC"));
    }

    #[test]
    fn test_non_ascii() {
        assert_eq!("😀NO", rot13("😀AB"));
    }

    #[test]
    fn test_twice() {
        assert_eq!("ABCD", rot13(&rot13("ABCD")));
    }
}
}

rot13第二种实现

#![allow(unused)]
fn main() {
pub fn another_rot13(text: &str) -> String {
    let input = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz";
    let output = "NOPQRSTUVWXYZABCDEFGHIJKLMnopqrstuvwxyzabcdefghijklm";
    text.chars()
        .map(|c| match input.find(c) {
            Some(i) => output.chars().nth(i).unwrap(),
            None => c,
        })
        .collect()
}

#[cfg(test)]
mod tests {
    // Note this useful idiom: importing names from outer (for mod tests) scope.
    use super::*;

    #[test]
    fn test_simple() {
        assert_eq!(another_rot13("ABCzyx"), "NOPmlk");
    }

    #[test]
    fn test_every_alphabet_with_space() {
        assert_eq!(
            another_rot13("The quick brown fox jumps over the lazy dog"),
            "Gur dhvpx oebja sbk whzcf bire gur ynml qbt"
        );
    }

    #[test]
    fn test_non_alphabet() {
        assert_eq!(another_rot13("🎃 Jack-o'-lantern"), "🎃 Wnpx-b'-ynagrea");
    }
}
}

sha256加密

#![allow(unused)]
fn main() {
//! SHA-2 (256 Bit)

struct BufState {
    data: Vec<u8>,
    len: usize,
    total_len: usize,
    single: bool,
    total: bool,
}

pub fn sha256(data: &[u8]) -> [u8; 32] {
    let mut hash: [u8; 32] = [0; 32];

    let mut h: [u32; 8] = [
        0x6a09e667, 0xbb67ae85, 0x3c6ef372, 0xa54ff53a, 0x510e527f, 0x9b05688c, 0x1f83d9ab,
        0x5be0cd19,
    ];

    let k: [u32; 64] = [
        0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4,
        0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe,
        0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f,
        0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7,
        0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc,
        0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b,
        0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116,
        0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
        0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7,
        0xc67178f2,
    ];

    let mut chunk: [u8; 64] = [0; 64];

    let mut state: BufState = BufState {
        data: (*data).to_owned(),
        len: data.len(),
        total_len: data.len(),
        single: false,
        total: false,
    };

    while calc_chunk(&mut chunk, &mut state) {
        let mut ah: [u32; 8] = h;
        let mut w: [u32; 16] = [0; 16];
        for i in 0..4 {
            for j in 0..16 {
                if i == 0 {
                    w[j] = ((chunk[j * 4] as u32) << 24)
                        | ((chunk[j * 4 + 1] as u32) << 16)
                        | ((chunk[j * 4 + 2] as u32) << 8)
                        | (chunk[j * 4 + 3] as u32);
                } else {
                    let s0 = (w[(j + 1) & 0xf].rotate_right(7) ^ w[(j + 1) & 0xf].rotate_right(18))
                        ^ (w[(j + 1) & 0xf] >> 3);
                    let s1 = w[(j + 14) & 0xf].rotate_right(17)
                        ^ w[(j + 14) & 0xf].rotate_right(19)
                        ^ (w[(j + 14) & 0xf] >> 10);
                    w[j] = w[j]
                        .wrapping_add(s0)
                        .wrapping_add(w[(j + 9) & 0xf])
                        .wrapping_add(s1);
                }

                let s1: u32 =
                    ah[4].rotate_right(6) ^ ah[4].rotate_right(11) ^ ah[4].rotate_right(25);
                let ch: u32 = (ah[4] & ah[5]) ^ (!ah[4] & ah[6]);
                let temp1: u32 = ah[7]
                    .wrapping_add(s1)
                    .wrapping_add(ch)
                    .wrapping_add(k[i << 4 | j])
                    .wrapping_add(w[j]);
                let s0: u32 =
                    ah[0].rotate_right(2) ^ ah[0].rotate_right(13) ^ ah[0].rotate_right(22);
                let maj: u32 = (ah[0] & ah[1]) ^ (ah[0] & ah[2]) ^ (ah[1] & ah[2]);
                let temp2: u32 = s0.wrapping_add(maj);

                ah[7] = ah[6];
                ah[6] = ah[5];
                ah[5] = ah[4];
                ah[4] = ah[3].wrapping_add(temp1);
                ah[3] = ah[2];
                ah[2] = ah[1];
                ah[1] = ah[0];
                ah[0] = temp1.wrapping_add(temp2);
            }
        }

        for i in 0..8 {
            h[i] = h[i].wrapping_add(ah[i]);
        }
        chunk = [0; 64];
    }

    for i in 0..8 {
        hash[i * 4] = (h[i] >> 24) as u8;
        hash[i * 4 + 1] = (h[i] >> 16) as u8;
        hash[i * 4 + 2] = (h[i] >> 8) as u8;
        hash[i * 4 + 3] = h[i] as u8;
    }

    hash
}

fn calc_chunk(chunk: &mut [u8; 64], state: &mut BufState) -> bool {
    if state.total {
        return false;
    }

    if state.len >= 64 {
        for x in chunk {
            *x = state.data[0];
            state.data.remove(0);
        }
        state.len -= 64;
        return true;
    }

    let remaining: usize = state.data.len();
    let space: usize = 64 - remaining;
    for x in chunk.iter_mut().take(state.data.len()) {
        *x = state.data[0];
        state.data.remove(0);
    }

    if !state.single {
        chunk[remaining] = 0x80;
        state.single = true;
    }

    if space >= 8 {
        let mut len = state.total_len;
        chunk[63] = (len << 3) as u8;
        len >>= 5;
        for i in 1..8 {
            chunk[(63 - i)] = len as u8;
            len >>= 8;
        }
        state.total = true;
    }

    true
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn empty() {
        assert_eq!(
            sha256(&Vec::new()),
            [
                0xe3, 0xb0, 0xc4, 0x42, 0x98, 0xfc, 0x1c, 0x14, 0x9a, 0xfb, 0xf4, 0xc8, 0x99, 0x6f,
                0xb9, 0x24, 0x27, 0xae, 0x41, 0xe4, 0x64, 0x9b, 0x93, 0x4c, 0xa4, 0x95, 0x99, 0x1b,
                0x78, 0x52, 0xb8, 0x55
            ]
        );
    }

    #[test]
    fn ascii() {
        assert_eq!(
            sha256(&b"The quick brown fox jumps over the lazy dog".to_vec()),
            [
                0xD7, 0xA8, 0xFB, 0xB3, 0x07, 0xD7, 0x80, 0x94, 0x69, 0xCA, 0x9A, 0xBC, 0xB0, 0x08,
                0x2E, 0x4F, 0x8D, 0x56, 0x51, 0xE4, 0x6D, 0x3C, 0xDB, 0x76, 0x2D, 0x02, 0xD0, 0xBF,
                0x37, 0xC9, 0xE5, 0x92
            ]
        )
    }

    #[test]
    fn ascii_avalanche() {
        assert_eq!(
            sha256(&b"The quick brown fox jumps over the lazy dog.".to_vec()),
            [
                0xEF, 0x53, 0x7F, 0x25, 0xC8, 0x95, 0xBF, 0xA7, 0x82, 0x52, 0x65, 0x29, 0xA9, 0xB6,
                0x3D, 0x97, 0xAA, 0x63, 0x15, 0x64, 0xD5, 0xD7, 0x89, 0xC2, 0xB7, 0x65, 0x44, 0x8C,
                0x86, 0x35, 0xFB, 0x6C
            ]
        )
    }
}
}

vigenere加密

#![allow(unused)]
fn main() {
//! Vigenère Cipher
//!
//! # Algorithm
//!
//! Rotate each ascii character by the offset of the corresponding key character.
//! When we reach the last key character, we start over from the first one.
//! This implementation does not rotate unicode characters.

/// Vigenère cipher to rotate plain_text text by key and return an owned String.
pub fn vigenere(plain_text: &str, key: &str) -> String {
    // Remove all unicode and non-ascii characters from key
    let key: String = key.chars().filter(|&c| c.is_ascii_alphabetic()).collect();
    key.to_ascii_lowercase();

    let key_len = key.len();
    if key_len == 0 {
        return String::from(plain_text);
    }

    let mut index = 0;

    plain_text
        .chars()
        .map(|c| {
            if c.is_ascii_alphabetic() {
                let first = if c.is_ascii_lowercase() { b'a' } else { b'A' };
                let shift = key.as_bytes()[index % key_len] - b'a';
                index += 1;
                // modulo the distance to keep character range
                (first + (c as u8 + shift - first) % 26) as char
            } else {
                c
            }
        })
        .collect()
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn empty() {
        assert_eq!(vigenere("", "test"), "");
    }

    #[test]
    fn vigenere_base() {
        assert_eq!(
            vigenere("LoremIpsumDolorSitAmet", "base"),
            "MojinIhwvmVsmojWjtSqft"
        );
    }

    #[test]
    fn vigenere_with_spaces() {
        assert_eq!(
            vigenere(
                "Lorem ipsum dolor sit amet, consectetur adipiscing elit.",
                "spaces"
            ),
            "Ddrgq ahhuo hgddr uml sbev, ggfheexwljr chahxsemfy tlkx."
        );
    }

    #[test]
    fn vigenere_unicode_and_numbers() {
        assert_eq!(
            vigenere("1 Lorem ⏳ ipsum dolor sit amet Ѡ", "unicode"),
            "1 Fbzga ⏳ ltmhu fcosl fqv opin Ѡ"
        );
    }

    #[test]
    fn vigenere_unicode_key() {
        assert_eq!(
            vigenere("Lorem ipsum dolor sit amet", "😉 key!"),
            "Vspoq gzwsw hmvsp cmr kqcd"
        );
    }

    #[test]
    fn vigenere_empty_key() {
        assert_eq!(vigenere("Lorem ipsum", ""), "Lorem ipsum");
    }
}
}

xor

#![allow(unused)]
fn main() {
pub fn xor(text: &str, key: u8) -> String {
    text.chars().map(|c| ((c as u8) ^ key) as char).collect()
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_simple() {
        let test_string = "test string";
        let ciphered_text = xor(test_string, 32);
        assert_eq!(test_string, xor(&ciphered_text, 32));
    }

    #[test]
    fn test_every_alphabet_with_space() {
        let test_string = "The quick brown fox jumps over the lazy dog";
        let ciphered_text = xor(test_string, 64);
        assert_eq!(test_string, xor(&ciphered_text, 64));
    }
}
}

凸包算法

#![allow(unused)]
fn main() {
use std::cmp::Ordering::Equal;

fn sort_by_min_angle(pts: &[(f64, f64)], min: &(f64, f64)) -> Vec<(f64, f64)> {
    let mut points: Vec<(f64, f64, (f64, f64))> = pts
        .iter()
        .map(|x| {
            (
                ((x.1 - min.1) as f64).atan2((x.0 - min.0) as f64),
                // angle
                ((x.1 - min.1) as f64).hypot((x.0 - min.0) as f64),
                // distance (we want the closest to be first)
                *x,
            )
        })
        .collect();
    points.sort_by(|a, b| a.partial_cmp(b).unwrap_or(Equal));
    points.into_iter().map(|x| x.2).collect()
}

// calculates the z coordinate of the vector product of vectors ab and ac
fn calc_z_coord_vector_product(a: &(f64, f64), b: &(f64, f64), c: &(f64, f64)) -> f64 {
    (b.0 - a.0) * (c.1 - a.1) - (c.0 - a.0) * (b.1 - a.1)
}

/*
    If three points are aligned and are part of the convex hull then the three are kept.
    If one doesn't want to keep those points, it is easy to iterate the answer and remove them.
    The first point is the one with the lowest y-coordinate and the lowest x-coordinate.
    Points are then given counter-clockwise, and the closest one is given first if needed.
*/
pub fn convex_hull_graham(pts: &[(f64, f64)]) -> Vec<(f64, f64)> {
    if pts.is_empty() {
        return vec![];
    }

    let mut stack: Vec<(f64, f64)> = vec![];
    let min = pts
        .iter()
        .min_by(|a, b| {
            let ord = a.1.partial_cmp(&b.1).unwrap_or(Equal);
            match ord {
                Equal => a.0.partial_cmp(&b.0).unwrap_or(Equal),
                o => o,
            }
        })
        .unwrap();
    let points = sort_by_min_angle(pts, min);

    if points.len() <= 3 {
        return points;
    }

    for point in points {
        while stack.len() > 1
            && calc_z_coord_vector_product(&stack[stack.len() - 2], &stack[stack.len() - 1], &point)
                < 0.
        {
            stack.pop();
        }
        stack.push(point);
    }

    stack
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn empty() {
        assert_eq!(convex_hull_graham(&vec![]), vec![]);
    }

    #[test]
    fn not_enough_points() {
        let list = vec![(0f64, 0f64)];
        assert_eq!(convex_hull_graham(&list), list);
    }

    #[test]
    fn not_enough_points1() {
        let list = vec![(2f64, 2f64), (1f64, 1f64), (0f64, 0f64)];
        let ans = vec![(0f64, 0f64), (1f64, 1f64), (2f64, 2f64)];
        assert_eq!(convex_hull_graham(&list), ans);
    }

    #[test]
    fn not_enough_points2() {
        let list = vec![(2f64, 2f64), (1f64, 2f64), (0f64, 0f64)];
        let ans = vec![(0f64, 0f64), (2f64, 2f64), (1f64, 2f64)];
        assert_eq!(convex_hull_graham(&list), ans);
    }

    #[test]
    // from https://codegolf.stackexchange.com/questions/11035/find-the-convex-hull-of-a-set-of-2d-points
    fn lots_of_points() {
        let list = vec![
            (4.4, 14.),
            (6.7, 15.25),
            (6.9, 12.8),
            (2.1, 11.1),
            (9.5, 14.9),
            (13.2, 11.9),
            (10.3, 12.3),
            (6.8, 9.5),
            (3.3, 7.7),
            (0.6, 5.1),
            (5.3, 2.4),
            (8.45, 4.7),
            (11.5, 9.6),
            (13.8, 7.3),
            (12.9, 3.1),
            (11., 1.1),
        ];
        let ans = vec![
            (11., 1.1),
            (12.9, 3.1),
            (13.8, 7.3),
            (13.2, 11.9),
            (9.5, 14.9),
            (6.7, 15.25),
            (4.4, 14.),
            (2.1, 11.1),
            (0.6, 5.1),
            (5.3, 2.4),
        ];

        assert_eq!(convex_hull_graham(&list), ans);
    }

    #[test]
    // from https://codegolf.stackexchange.com/questions/11035/find-the-convex-hull-of-a-set-of-2d-points
    fn lots_of_points2() {
        let list = vec![
            (1., 0.),
            (1., 1.),
            (1., -1.),
            (0.68957, 0.283647),
            (0.909487, 0.644276),
            (0.0361877, 0.803816),
            (0.583004, 0.91555),
            (-0.748169, 0.210483),
            (-0.553528, -0.967036),
            (0.316709, -0.153861),
            (-0.79267, 0.585945),
            (-0.700164, -0.750994),
            (0.452273, -0.604434),
            (-0.79134, -0.249902),
            (-0.594918, -0.397574),
            (-0.547371, -0.434041),
            (0.958132, -0.499614),
            (0.039941, 0.0990732),
            (-0.891471, -0.464943),
            (0.513187, -0.457062),
            (-0.930053, 0.60341),
            (0.656995, 0.854205),
        ];
        let ans = vec![
            (1., -1.),
            (1., 0.),
            (1., 1.),
            (0.583004, 0.91555),
            (0.0361877, 0.803816),
            (-0.930053, 0.60341),
            (-0.891471, -0.464943),
            (-0.700164, -0.750994),
            (-0.553528, -0.967036),
        ];

        assert_eq!(convex_hull_graham(&list), ans);
    }
}
}

汉诺塔算法

#![allow(unused)]
fn main() {
pub fn hanoi(n: i32, from: i32, to: i32, via: i32, moves: &mut Vec<(i32, i32)>) {
    if n > 0 {
        hanoi(n - 1, from, via, to, moves);
        moves.push((from, to));
        hanoi(n - 1, via, to, from, moves);
    }
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn hanoi_simple() {
        let correct_solution: Vec<(i32, i32)> =
            vec![(1, 3), (1, 2), (3, 2), (1, 3), (2, 1), (2, 3), (1, 3)];
        let mut our_solution: Vec<(i32, i32)> = Vec::new();
        hanoi(3, 1, 3, 2, &mut our_solution);
        assert_eq!(correct_solution, our_solution);
    }
}
}

K-Means算法

#![allow(unused)]
fn main() {
// Macro to implement kmeans for both f64 and f32 without writing everything
// twice or importing the `num` crate
macro_rules! impl_kmeans {
    ($kind: ty, $modname: ident) => {
        // Since we can't overload methods in rust, we have to use namespacing
        pub mod $modname {
            use std::$modname::INFINITY;

            /// computes sum of squared deviation between two identically sized vectors
            /// `x`, and `y`.
            fn distance(x: &[$kind], y: &[$kind]) -> $kind {
                x.iter()
                    .zip(y.iter())
                    .fold(0.0, |dist, (&xi, &yi)| dist + (xi - yi).powi(2))
            }

            /// Returns a vector containing the indices z<sub>i</sub> in {0, ..., K-1} of
            /// the centroid nearest to each datum.
            fn nearest_centroids(xs: &[Vec<$kind>], centroids: &[Vec<$kind>]) -> Vec<usize> {
                xs.iter()
                    .map(|xi| {
                        // Find the argmin by folding using a tuple containing the argmin
                        // and the minimum distance.
                        let (argmin, _) = centroids.iter().enumerate().fold(
                            (0_usize, INFINITY),
                            |(min_ix, min_dist), (ix, ci)| {
                                let dist = distance(xi, ci);
                                if dist < min_dist {
                                    (ix, dist)
                                } else {
                                    (min_ix, min_dist)
                                }
                            },
                        );
                        argmin
                    })
                    .collect()
            }

            /// Recompute the centroids given the current clustering
            fn recompute_centroids(
                xs: &[Vec<$kind>],
                clustering: &[usize],
                k: usize,
            ) -> Vec<Vec<$kind>> {
                let ndims = xs[0].len();

                // NOTE: Kind of inefficient because we sweep all the data from each of the
                // k centroids.
                (0..k)
                    .map(|cluster_ix| {
                        let mut centroid: Vec<$kind> = vec![0.0; ndims];
                        let mut n_cluster: $kind = 0.0;
                        xs.iter().zip(clustering.iter()).for_each(|(xi, &zi)| {
                            if zi == cluster_ix {
                                n_cluster += 1.0;
                                xi.iter().enumerate().for_each(|(j, &x_ij)| {
                                    centroid[j] += x_ij;
                                });
                            }
                        });
                        centroid.iter().map(|&c_j| c_j / n_cluster).collect()
                    })
                    .collect()
            }

            /// Assign the N D-dimensional data, `xs`, to `k` clusters using K-Means clustering
            pub fn kmeans(xs: Vec<Vec<$kind>>, k: usize) -> Vec<usize> {
                assert!(xs.len() >= k);

                // Rather than pulling in a dependency to radomly select the staring
                // points for the centroids, we're going to deterministally choose them by
                // slecting evenly spaced points in `xs`
                let n_per_cluster: usize = xs.len() / k;
                let centroids: Vec<Vec<$kind>> =
                    (0..k).map(|j| xs[j * n_per_cluster].clone()).collect();

                let mut clustering = nearest_centroids(&xs, &centroids);

                loop {
                    let centroids = recompute_centroids(&xs, &clustering, k);
                    let new_clustering = nearest_centroids(&xs, &centroids);

                    // loop until the clustering doesn't change after the new centroids are computed
                    if new_clustering
                        .iter()
                        .zip(clustering.iter())
                        .all(|(&za, &zb)| za == zb)
                    {
                        // We need to use `return` to break out of the `loop`
                        return clustering;
                    } else {
                        clustering = new_clustering;
                    }
                }
            }
        }
    };
}

// generate code for kmeans for f32 and f64 data
impl_kmeans!(f64, f64);
impl_kmeans!(f32, f32);

#[cfg(test)]
mod test {
    use self::super::f64::kmeans;

    #[test]
    fn easy_univariate_clustering() {
        let xs: Vec<Vec<f64>> = vec![
            vec![-1.1],
            vec![-1.2],
            vec![-1.3],
            vec![-1.4],
            vec![1.1],
            vec![1.2],
            vec![1.3],
            vec![1.4],
        ];
        let clustering = kmeans(xs, 2);
        assert_eq!(clustering, vec![0, 0, 0, 0, 1, 1, 1, 1]);
    }

    #[test]
    fn easy_univariate_clustering_odd_number_of_data() {
        let xs: Vec<Vec<f64>> = vec![
            vec![-1.1],
            vec![-1.2],
            vec![-1.3],
            vec![-1.4],
            vec![1.1],
            vec![1.2],
            vec![1.3],
            vec![1.4],
            vec![1.5],
        ];
        let clustering = kmeans(xs, 2);
        assert_eq!(clustering, vec![0, 0, 0, 0, 1, 1, 1, 1, 1]);
    }

    #[test]
    fn easy_bivariate_clustering() {
        let xs: Vec<Vec<f64>> = vec![
            vec![-1.1, 0.2],
            vec![-1.2, 0.3],
            vec![-1.3, 0.1],
            vec![-1.4, 0.4],
            vec![1.1, -1.1],
            vec![1.2, -1.0],
            vec![1.3, -1.2],
            vec![1.4, -1.3],
        ];
        let clustering = kmeans(xs, 2);
        assert_eq!(clustering, vec![0, 0, 0, 0, 1, 1, 1, 1]);
    }

    #[test]
    fn high_dims() {
        let xs: Vec<Vec<f64>> = vec![
            vec![-2.7825343, -1.7604825, -5.5550113, -2.9752946, -2.7874138],
            vec![-2.9847919, -3.8209332, -2.1531757, -2.2710119, -2.3582877],
            vec![-3.0109320, -2.2366132, -2.8048492, -1.2632331, -4.5755581],
            vec![-2.8432186, -1.0383805, -2.2022826, -2.7435962, -2.0013399],
            vec![-2.6638082, -3.5520086, -1.3684702, -2.1562444, -1.3186447],
            vec![1.7409171, 1.9687576, 4.7162628, 4.5743537, 3.7905611],
            vec![3.2932369, 2.8508700, 2.5580937, 2.0437325, 4.2192562],
            vec![2.5843321, 2.8329818, 2.1329531, 3.2562319, 2.4878733],
            vec![2.1859638, 3.2880048, 3.7018615, 2.3641232, 1.6281994],
            vec![2.6201773, 0.9006588, 2.6774097, 1.8188620, 1.6076493],
        ];

        let clustering = kmeans(xs, 2);
        assert_eq!(clustering, vec![0, 0, 0, 0, 0, 1, 1, 1, 1, 1]);
    }
}
}

N皇后算法

#[allow(unused_imports)]
use std::env::args;

#[allow(dead_code)]
fn main() {
    let mut board_width = 0;

    for arg in args() {
        board_width = match arg.parse() {
            Ok(x) => x,
            _ => 0,
        };

        if board_width != 0 {
            break;
        }
    }

    if board_width < 4 {
        println!(
            "Running algorithm with 8 as a default. Specify an alternative Chess board size for \
             N-Queens as a command line argument.\n"
        );
        board_width = 8;
    }

    let board = match nqueens(board_width) {
        Ok(success) => success,
        Err(err) => panic!("{}", err),
    };

    println!("N-Queens {} by {} board result:", board_width, board_width);
    print_board(&board);
}

/*
The n-Queens search is a backtracking algorithm. Each row of the Chess board where a Queen is
placed is dependent on all earlier rows. As only one Queen can fit per row, a one-dimensional
integer array is used to represent the Queen's offset on each row.
*/
pub fn nqueens(board_width: i64) -> Result<Vec<i64>, &'static str> {
    let mut board_rows = vec![0; board_width as usize];
    let mut conflict;
    let mut current_row = 0;

    //Process by row up to the current active row
    loop {
        conflict = false;

        //Column review of previous rows
        for review_index in 0..current_row {
            //Calculate the diagonals of earlier rows where a Queen would be a conflict
            let left = board_rows[review_index] - (current_row as i64 - review_index as i64);
            let right = board_rows[review_index] + (current_row as i64 - review_index as i64);

            if board_rows[current_row] == board_rows[review_index]
                || (left >= 0 && left == board_rows[current_row])
                || (right < board_width as i64 && right == board_rows[current_row])
            {
                conflict = true;
                break;
            }
        }

        match conflict {
            true => {
                board_rows[current_row] += 1;

                if current_row == 0 && board_rows[current_row] == board_width {
                    return Err("No solution exists for specificed board size.");
                }

                while board_rows[current_row] == board_width {
                    board_rows[current_row] = 0;

                    if current_row == 0 {
                        return Err("No solution exists for specificed board size.");
                    }

                    current_row -= 1;
                    board_rows[current_row] += 1;
                }
            }
            _ => {
                current_row += 1;

                if current_row as i64 == board_width {
                    break;
                }
            }
        }
    }

    Ok(board_rows)
}

fn print_board(board: &[i64]) {
    for row in 0..board.len() {
        print!("{}\t", board[row as usize]);

        for column in 0..board.len() as i64 {
            if board[row as usize] == column {
                print!("Q");
            } else {
                print!(".");
            }
        }
        println!();
    }
}

#[cfg(test)]
mod test {
    use super::*;

    fn check_board(board: &Vec<i64>) -> bool {
        for current_row in 0..board.len() {
            //Column review
            for review_index in 0..current_row {
                //Look for any conflict.
                let left = board[review_index] - (current_row as i64 - review_index as i64);
                let right = board[review_index] + (current_row as i64 - review_index as i64);

                if board[current_row] == board[review_index]
                    || (left >= 0 && left == board[current_row])
                    || (right < board.len() as i64 && right == board[current_row])
                {
                    return false;
                }
            }
        }
        true
    }

    #[test]
    fn test_board_size_4() {
        let board = nqueens(4).expect("Error propagated.");
        assert_eq!(board, vec![1, 3, 0, 2]);
        assert!(check_board(&board));
    }

    #[test]
    fn test_board_size_7() {
        let board = nqueens(7).expect("Error propagated.");
        assert_eq!(board, vec![0, 2, 4, 6, 1, 3, 5]);
        assert!(check_board(&board));
    }
}

两数之和

#![allow(unused)]
fn main() {
use std::collections::HashMap;
use std::convert::TryInto;

// Given an array of integers nums and an integer target,
// return indices of the two numbers such that they add up to target.

pub fn two_sum(nums: Vec<i32>, target: i32) -> Vec<i32> {
    let mut hash_map: HashMap<i32, i32> = HashMap::new();

    for (i, item) in nums.iter().enumerate() {
        match hash_map.get(&(target - item)) {
            Some(value) => {
                return vec![i.try_into().unwrap(), *value];
            }
            None => {
                hash_map.insert(*item, i.try_into().unwrap());
            }
        }
    }

    vec![]
}

#[cfg(test)]
mod test {
    use super::*;

    #[test]
    fn test() {
        let nums = vec![2, 7, 11, 15];
        assert_eq!(two_sum(nums, 9), vec![1, 0]);

        let nums = vec![3, 2, 4];
        assert_eq!(two_sum(nums, 6), vec![2, 1]);

        let nums = vec![3, 3];
        assert_eq!(two_sum(nums, 6), vec![1, 0]);
    }
}
}

数据结构

数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关

在计算机科学的发展过程中，数据结构也随之发展。程序设计中常用的数据结构包括如下几个。

1. 数组(Array) 数组是一种聚合数据类型，它是将具有相同类型的若干变量有序地组织在一起的集合。数组可以说是最基本的数据结构，在各种编程语言中都有对应。一个数组可以分解为多个数组元素，按照数据元素的类型，数组可以分为整型数组、字符型数组、浮点型数组、指针数组和结构数组等。数组还可以有一维、二维以及多维等表现形式。

2. 栈( Stack) 栈是一种特殊的线性表，它只能在一个表的一个固定端进行数据结点的插入和删除操作。栈按照后进先出的原则来存储数据，也就是说，先插入的数据将被压入栈底，最后插入的数据在栈顶，读出数据时，从栈顶开始逐个读出。栈在汇编语言程序中，经常用于重要数据的现场保护。栈中没有数据时，称为空栈。

3. 队列(Queue) 队列和栈类似，也是一种特殊的线性表。和栈不同的是，队列只允许在表的一端进行插入操作，而在另一端进行删除操作。一般来说，进行插入操作的一端称为队尾，进行删除操作的一端称为队头。队列中没有元素时，称为空队列。

4. 链表( Linked List) 链表是一种数据元素按照链式存储结构进行存储的数据结构，这种存储结构具有在物理上存在非连续的特点。链表由一系列数据结点构成，每个数据结点包括数据域和指针域两部分。其中，指针域保存了数据结构中下一个元素存放的地址。链表结构中数据元素的逻辑顺序是通过链表中的指针链接次序来实现的。

5. 树( Tree) 树是典型的非线性结构，它是包括，2个结点的有穷集合K。在树结构中，有且仅有一个根结点，该结点没有前驱结点。在树结构中的其他结点都有且仅有一个前驱结点，而且可以有两个后继结点，m≥0。

6. 图(Graph) 图是另一种非线性数据结构。在图结构中，数据结点一般称为顶点，而边是顶点的有序偶对。如果两个顶点之间存在一条边，那么就表示这两个顶点具有相邻关系。

7.堆(Heap) 堆是一种特殊的树形数据结构，一般讨论的堆都是二叉堆。堆的特点是根结点的值是所有结点中最小的或者最大的，并且根结点的两个子树也是一个堆结构。

8.散列表(Hash) 散列表源自于散列函数(Hash function)，其思想是如果在结构中存在关键字和T相等的记录，那么必定在F(T)的存储位置可以找到该记录，这样就可以不用进行比较操作而直接取得所查记录。

B树

B-Trees are version of 2-3 trees, which are self-balancing. They are used to improve Disk reads and have a complexity of O(log(n)), for every tree operations.The number of Childrens/Keys a particular node has, is determined by the Branching Factor/Degree of that tree. B-Trees will always have sorted keys.

• Branching Factor(B) / Degree (D): If B = n, n <= Children per Node < 2(n), n-1 <= Keys per Node < 2(n) - 1

Properties

• Worst/Average case performance for all operations O(log n)
• Space complexity O(n)

#![allow(unused)]
fn main() {
use std::convert::TryFrom;
use std::fmt::Debug;
use std::mem;

struct Node<T> {
    keys: Vec<T>,
    children: Vec<Node<T>>,
}

pub struct BTree<T> {
    root: Node<T>,
    props: BTreeProps,
}

// Why to need a different Struct for props...
// Check - http://smallcultfollowing.com/babysteps/blog/2018/11/01/after-nll-interprocedural-conflicts/#fnref:improvement
struct BTreeProps {
    degree: usize,
    max_keys: usize,
    mid_key_index: usize,
}

impl<T> Node<T>
where
    T: Ord,
{
    fn new(degree: usize, _keys: Option<Vec<T>>, _children: Option<Vec<Node<T>>>) -> Self {
        Node {
            keys: match _keys {
                Some(_keys) => _keys,
                None => Vec::with_capacity(degree - 1),
            },
            children: match _children {
                Some(_children) => _children,
                None => Vec::with_capacity(degree),
            },
        }
    }

    fn is_leaf(&self) -> bool {
        self.children.is_empty()
    }
}

impl BTreeProps {
    fn new(degree: usize) -> Self {
        BTreeProps {
            degree,
            max_keys: degree - 1,
            mid_key_index: (degree - 1) / 2,
        }
    }

    fn is_maxed_out<T: Ord + Copy>(&self, node: &Node<T>) -> bool {
        node.keys.len() == self.max_keys
    }

    // Split Child expects the Child Node to be full
    /// Move the middle_key to parent node and split the child_node's
    /// keys/chilren_nodes into half
    fn split_child<T: Ord + Copy + Default>(&self, parent: &mut Node<T>, child_index: usize) {
        let child = &mut parent.children[child_index];
        let middle_key = child.keys[self.mid_key_index];
        let right_keys = match child.keys.split_off(self.mid_key_index).split_first() {
            Some((_first, _others)) => {
                // We don't need _first, as it will move to parent node.
                _others.to_vec()
            }
            None => Vec::with_capacity(self.max_keys),
        };
        let right_children = if !child.is_leaf() {
            Some(child.children.split_off(self.mid_key_index + 1))
        } else {
            None
        };
        let new_child_node: Node<T> = Node::new(self.degree, Some(right_keys), right_children);

        parent.keys.insert(child_index, middle_key);
        parent.children.insert(child_index + 1, new_child_node);
    }

    fn insert_non_full<T: Ord + Copy + Default>(&mut self, node: &mut Node<T>, key: T) {
        let mut index: isize = isize::try_from(node.keys.len()).ok().unwrap() - 1;
        while index >= 0 && node.keys[index as usize] >= key {
            index -= 1;
        }

        let mut u_index: usize = usize::try_from(index + 1).ok().unwrap();
        if node.is_leaf() {
            // Just insert it, as we know this method will be called only when node is not full
            node.keys.insert(u_index, key);
        } else {
            if self.is_maxed_out(&node.children[u_index]) {
                self.split_child(node, u_index);
                if node.keys[u_index] < key {
                    u_index += 1;
                }
            }

            self.insert_non_full(&mut node.children[u_index], key);
        }
    }

    fn traverse_node<T: Ord + Debug>(&self, node: &Node<T>, depth: usize) {
        if node.is_leaf() {
            print!(" {0:{<1$}{2:?}{0:}<1$} ", "", depth, node.keys);
        } else {
            let _depth = depth + 1;
            for (index, key) in node.keys.iter().enumerate() {
                self.traverse_node(&node.children[index], _depth);
                // Check https://doc.rust-lang.org/std/fmt/index.html
                // And https://stackoverflow.com/a/35280799/2849127
                print!("{0:{<1$}{2:?}{0:}<1$}", "", depth, key);
            }
            self.traverse_node(node.children.last().unwrap(), _depth);
        }
    }
}

impl<T> BTree<T>
where
    T: Ord + Copy + Debug + Default,
{
    pub fn new(branch_factor: usize) -> Self {
        let degree = 2 * branch_factor;
        BTree {
            root: Node::new(degree, None, None),
            props: BTreeProps::new(degree),
        }
    }

    pub fn insert(&mut self, key: T) {
        if self.props.is_maxed_out(&self.root) {
            // Create an empty root and split the old root...
            let mut new_root = Node::new(self.props.degree, None, None);
            mem::swap(&mut new_root, &mut self.root);
            self.root.children.insert(0, new_root);
            self.props.split_child(&mut self.root, 0);
        }
        self.props.insert_non_full(&mut self.root, key);
    }

    pub fn traverse(&self) {
        self.props.traverse_node(&self.root, 0);
        println!();
    }

    pub fn search(&self, key: T) -> bool {
        let mut current_node = &self.root;
        let mut index: isize;
        loop {
            index = isize::try_from(current_node.keys.len()).ok().unwrap() - 1;
            while index >= 0 && current_node.keys[index as usize] > key {
                index -= 1;
            }

            let u_index: usize = usize::try_from(index + 1).ok().unwrap();
            if index >= 0 && current_node.keys[u_index - 1] == key {
                break true;
            } else if current_node.is_leaf() {
                break false;
            } else {
                current_node = &current_node.children[u_index];
            }
        }
    }
}

#[cfg(test)]
mod test {
    use super::BTree;

    #[test]
    fn test_search() {
        let mut tree = BTree::new(2);
        tree.insert(10);
        tree.insert(20);
        tree.insert(30);
        tree.insert(5);
        tree.insert(6);
        tree.insert(7);
        tree.insert(11);
        tree.insert(12);
        tree.insert(15);
        assert!(tree.search(15));
        assert_eq!(tree.search(16), false);
    }
}
}

二叉树

#![allow(unused)]
fn main() {
use std::cmp::Ordering;
use std::ops::Deref;

/// This struct implements as Binary Search Tree (BST), which is a
/// simple data structure for storing sorted data
pub struct BinarySearchTree<T>
where
    T: Ord,
{
    value: Option<T>,
    left: Option<Box<BinarySearchTree<T>>>,
    right: Option<Box<BinarySearchTree<T>>>,
}

impl<T> Default for BinarySearchTree<T>
where
    T: Ord,
{
    fn default() -> Self {
        Self::new()
    }
}

impl<T> BinarySearchTree<T>
where
    T: Ord,
{
    /// Create a new, empty BST
    pub fn new() -> BinarySearchTree<T> {
        BinarySearchTree {
            value: None,
            left: None,
            right: None,
        }
    }

    /// Find a value in this tree. Returns True iff value is in this
    /// tree, and false otherwise
    pub fn search(&self, value: &T) -> bool {
        match &self.value {
            Some(key) => {
                match key.cmp(value) {
                    Ordering::Equal => {
                        // key == value
                        true
                    }
                    Ordering::Greater => {
                        // key > value
                        match &self.left {
                            Some(node) => node.search(value),
                            None => false,
                        }
                    }
                    Ordering::Less => {
                        // key < value
                        match &self.right {
                            Some(node) => node.search(value),
                            None => false,
                        }
                    }
                }
            }
            None => false,
        }
    }

    /// Returns a new iterator which iterates over this tree in order
    pub fn iter(&self) -> impl Iterator<Item = &T> {
        BinarySearchTreeIter::new(self)
    }

    /// Insert a value into the appropriate location in this tree.
    pub fn insert(&mut self, value: T) {
        if self.value.is_none() {
            self.value = Some(value);
        } else {
            match &self.value {
                None => (),
                Some(key) => {
                    let target_node = if value < *key {
                        &mut self.left
                    } else {
                        &mut self.right
                    };
                    match target_node {
                        Some(ref mut node) => {
                            node.insert(value);
                        }
                        None => {
                            let mut node = BinarySearchTree::new();
                            node.insert(value);
                            *target_node = Some(Box::new(node));
                        }
                    }
                }
            }
        }
    }

    /// Returns the smallest value in this tree
    pub fn minimum(&self) -> Option<&T> {
        match &self.left {
            Some(node) => node.minimum(),
            None => match &self.value {
                Some(value) => Some(value),
                None => None,
            },
        }
    }

    /// Returns the largest value in this tree
    pub fn maximum(&self) -> Option<&T> {
        match &self.right {
            Some(node) => node.maximum(),
            None => match &self.value {
                Some(value) => Some(value),
                None => None,
            },
        }
    }

    /// Returns the largest value in this tree smaller than value
    pub fn floor(&self, value: &T) -> Option<&T> {
        match &self.value {
            Some(key) => {
                match key.cmp(value) {
                    Ordering::Greater => {
                        // key > value
                        match &self.left {
                            Some(node) => node.floor(value),
                            None => None,
                        }
                    }
                    Ordering::Less => {
                        // key < value
                        match &self.right {
                            Some(node) => {
                                let val = node.floor(value);
                                match val {
                                    Some(_) => val,
                                    None => Some(key),
                                }
                            }
                            None => Some(key),
                        }
                    }
                    Ordering::Equal => Some(key),
                }
            }
            None => None,
        }
    }

    /// Returns the smallest value in this tree larger than value
    pub fn ceil(&self, value: &T) -> Option<&T> {
        match &self.value {
            Some(key) => {
                match key.cmp(value) {
                    Ordering::Less => {
                        // key < value
                        match &self.right {
                            Some(node) => node.ceil(value),
                            None => None,
                        }
                    }
                    Ordering::Greater => {
                        // key > value
                        match &self.left {
                            Some(node) => {
                                let val = node.ceil(value);
                                match val {
                                    Some(_) => val,
                                    None => Some(key),
                                }
                            }
                            None => Some(key),
                        }
                    }
                    Ordering::Equal => {
                        // key == value
                        Some(key)
                    }
                }
            }
            None => None,
        }
    }
}

struct BinarySearchTreeIter<'a, T>
where
    T: Ord,
{
    stack: Vec<&'a BinarySearchTree<T>>,
}

impl<'a, T> BinarySearchTreeIter<'a, T>
where
    T: Ord,
{
    pub fn new(tree: &BinarySearchTree<T>) -> BinarySearchTreeIter<T> {
        let mut iter = BinarySearchTreeIter { stack: vec![tree] };
        iter.stack_push_left();
        iter
    }

    fn stack_push_left(&mut self) {
        while let Some(child) = &self.stack.last().unwrap().left {
            self.stack.push(child);
        }
    }
}

impl<'a, T> Iterator for BinarySearchTreeIter<'a, T>
where
    T: Ord,
{
    type Item = &'a T;

    fn next(&mut self) -> Option<&'a T> {
        if self.stack.is_empty() {
            None
        } else {
            let node = self.stack.pop().unwrap();
            if node.right.is_some() {
                self.stack.push(node.right.as_ref().unwrap().deref());
                self.stack_push_left();
            }
            node.value.as_ref()
        }
    }
}

#[cfg(test)]
mod test {
    use super::BinarySearchTree;

    fn prequel_memes_tree() -> BinarySearchTree<&'static str> {
        let mut tree = BinarySearchTree::new();
        tree.insert("hello there");
        tree.insert("general kenobi");
        tree.insert("you are a bold one");
        tree.insert("kill him");
        tree.insert("back away...I will deal with this jedi slime myself");
        tree.insert("your move");
        tree.insert("you fool");
        tree
    }

    #[test]
    fn test_search() {
        let tree = prequel_memes_tree();
        assert!(tree.search(&"hello there"));
        assert!(tree.search(&"you are a bold one"));
        assert!(tree.search(&"general kenobi"));
        assert!(tree.search(&"you fool"));
        assert!(tree.search(&"kill him"));
        assert!(
            !tree.search(&"but i was going to tosche station to pick up some power converters",)
        );
        assert!(!tree.search(&"only a sith deals in absolutes"));
        assert!(!tree.search(&"you underestimate my power"));
    }

    #[test]
    fn test_maximum_and_minimum() {
        let tree = prequel_memes_tree();
        assert_eq!(*tree.maximum().unwrap(), "your move");
        assert_eq!(
            *tree.minimum().unwrap(),
            "back away...I will deal with this jedi slime myself"
        );
        let mut tree2: BinarySearchTree<i32> = BinarySearchTree::new();
        assert!(tree2.maximum().is_none());
        assert!(tree2.minimum().is_none());
        tree2.insert(0);
        assert_eq!(*tree2.minimum().unwrap(), 0);
        assert_eq!(*tree2.maximum().unwrap(), 0);
        tree2.insert(-5);
        assert_eq!(*tree2.minimum().unwrap(), -5);
        assert_eq!(*tree2.maximum().unwrap(), 0);
        tree2.insert(5);
        assert_eq!(*tree2.minimum().unwrap(), -5);
        assert_eq!(*tree2.maximum().unwrap(), 5);
    }

    #[test]
    fn test_floor_and_ceil() {
        let tree = prequel_memes_tree();
        assert_eq!(*tree.floor(&"hello there").unwrap(), "hello there");
        assert_eq!(
            *tree
                .floor(&"these are not the droids you're looking for")
                .unwrap(),
            "kill him"
        );
        assert!(tree.floor(&"another death star").is_none());
        assert_eq!(*tree.floor(&"you fool").unwrap(), "you fool");
        assert_eq!(
            *tree.floor(&"but i was going to tasche station").unwrap(),
            "back away...I will deal with this jedi slime myself"
        );
        assert_eq!(
            *tree.floor(&"you underestimate my power").unwrap(),
            "you fool"
        );
        assert_eq!(*tree.floor(&"your new empire").unwrap(), "your move");
        assert_eq!(*tree.ceil(&"hello there").unwrap(), "hello there");
        assert_eq!(
            *tree
                .ceil(&"these are not the droids you're looking for")
                .unwrap(),
            "you are a bold one"
        );
        assert_eq!(
            *tree.ceil(&"another death star").unwrap(),
            "back away...I will deal with this jedi slime myself"
        );
        assert_eq!(*tree.ceil(&"you fool").unwrap(), "you fool");
        assert_eq!(
            *tree.ceil(&"but i was going to tasche station").unwrap(),
            "general kenobi"
        );
        assert_eq!(
            *tree.ceil(&"you underestimate my power").unwrap(),
            "your move"
        );
        assert!(tree.ceil(&"your new empire").is_none());
    }

    #[test]
    fn test_iterator() {
        let tree = prequel_memes_tree();
        let mut iter = tree.iter();
        assert_eq!(
            iter.next().unwrap(),
            &"back away...I will deal with this jedi slime myself"
        );
        assert_eq!(iter.next().unwrap(), &"general kenobi");
        assert_eq!(iter.next().unwrap(), &"hello there");
        assert_eq!(iter.next().unwrap(), &"kill him");
        assert_eq!(iter.next().unwrap(), &"you are a bold one");
        assert_eq!(iter.next().unwrap(), &"you fool");
        assert_eq!(iter.next().unwrap(), &"your move");
        assert_eq!(iter.next(), None);
        assert_eq!(iter.next(), None);
    }
}
}

avl树

An AVL Tree is a self-balancing binary search tree. The heights of any two sibling nodes must differ by at most one; the tree may rebalance itself after insertion or deletion to uphold this property.

Properties

• Worst/Average time complexity for basic operations: O(log n)
• Worst/Average space complexity: O(n)

#![allow(unused)]
fn main() {
use std::{
    cmp::{max, Ordering},
    iter::FromIterator,
    mem,
    ops::Not,
};

/// An internal node of an `AVLTree`.
struct AVLNode<T: Ord> {
    value: T,
    height: usize,
    left: Option<Box<AVLNode<T>>>,
    right: Option<Box<AVLNode<T>>>,
}

/// A set based on an AVL Tree.
///
/// An AVL Tree is a self-balancing binary search tree. It tracks the height of each node
/// and performs internal rotations to maintain a height difference of at most 1 between
/// each sibling pair.
pub struct AVLTree<T: Ord> {
    root: Option<Box<AVLNode<T>>>,
    length: usize,
}

/// Refers to the left or right subtree of an `AVLNode`.
#[derive(Clone, Copy)]
enum Side {
    Left,
    Right,
}

impl<T: Ord> AVLTree<T> {
    /// Creates an empty `AVLTree`.
    pub fn new() -> AVLTree<T> {
        AVLTree {
            root: None,
            length: 0,
        }
    }

    /// Returns `true` if the tree contains a value.
    pub fn contains(&self, value: &T) -> bool {
        let mut current = &self.root;
        while let Some(node) = current {
            current = match value.cmp(&node.value) {
                Ordering::Equal => return true,
                Ordering::Less => &node.left,
                Ordering::Greater => &node.right,
            }
        }
        false
    }

    /// Adds a value to the tree.
    ///
    /// Returns `true` if the tree did not yet contain the value.
    pub fn insert(&mut self, value: T) -> bool {
        let inserted = insert(&mut self.root, value);
        if inserted {
            self.length += 1;
        }
        inserted
    }

    /// Removes a value from the tree.
    ///
    /// Returns `true` if the tree contained the value.
    pub fn remove(&mut self, value: &T) -> bool {
        let removed = remove(&mut self.root, value);
        if removed {
            self.length -= 1;
        }
        removed
    }

    /// Returns the number of values in the tree.
    pub fn len(&self) -> usize {
        self.length
    }

    /// Returns `true` if the tree contains no values.
    pub fn is_empty(&self) -> bool {
        self.length == 0
    }

    /// Returns an iterator that visits the nodes in the tree in order.
    fn node_iter(&self) -> NodeIter<T> {
        let cap = self.root.as_ref().map_or(0, |n| n.height);
        let mut node_iter = NodeIter {
            stack: Vec::with_capacity(cap),
        };
        // Initialize stack with path to leftmost child
        let mut child = &self.root;
        while let Some(node) = child {
            node_iter.stack.push(node.as_ref());
            child = &node.left;
        }
        node_iter
    }

    /// Returns an iterator that visits the values in the tree in ascending order.
    pub fn iter(&self) -> Iter<T> {
        Iter {
            node_iter: self.node_iter(),
        }
    }
}

/// Recursive helper function for `AVLTree` insertion.
fn insert<T: Ord>(tree: &mut Option<Box<AVLNode<T>>>, value: T) -> bool {
    if let Some(node) = tree {
        let inserted = match value.cmp(&node.value) {
            Ordering::Equal => false,
            Ordering::Less => insert(&mut node.left, value),
            Ordering::Greater => insert(&mut node.right, value),
        };
        if inserted {
            node.rebalance();
        }
        inserted
    } else {
        *tree = Some(Box::new(AVLNode {
            value,
            height: 1,
            left: None,
            right: None,
        }));
        true
    }
}

/// Recursive helper function for `AVLTree` deletion.
fn remove<T: Ord>(tree: &mut Option<Box<AVLNode<T>>>, value: &T) -> bool {
    if let Some(node) = tree {
        let removed = match value.cmp(&node.value) {
            Ordering::Less => remove(&mut node.left, value),
            Ordering::Greater => remove(&mut node.right, value),
            Ordering::Equal => {
                *tree = match (node.left.take(), node.right.take()) {
                    (None, None) => None,
                    (Some(b), None) | (None, Some(b)) => Some(b),
                    (Some(left), Some(right)) => Some(merge(left, right)),
                };
                return true;
            }
        };
        if removed {
            node.rebalance();
        }
        removed
    } else {
        false
    }
}

/// Merges two trees and returns the root of the merged tree.
fn merge<T: Ord>(left: Box<AVLNode<T>>, right: Box<AVLNode<T>>) -> Box<AVLNode<T>> {
    let mut op_right = Some(right);
    // Guaranteed not to panic since right has at least one node
    let mut root = take_min(&mut op_right).unwrap();
    root.left = Some(left);
    root.right = op_right;
    root.rebalance();
    root
}

/// Removes the smallest node from the tree, if one exists.
fn take_min<T: Ord>(tree: &mut Option<Box<AVLNode<T>>>) -> Option<Box<AVLNode<T>>> {
    if let Some(mut node) = tree.take() {
        // Recurse along the left side
        if let Some(small) = take_min(&mut node.left) {
            // Took the smallest from below; update this node and put it back in the tree
            node.rebalance();
            *tree = Some(node);
            Some(small)
        } else {
            // Take this node and replace it with its right child
            *tree = node.right.take();
            Some(node)
        }
    } else {
        None
    }
}

impl<T: Ord> AVLNode<T> {
    /// Returns a reference to the left or right child.
    fn child(&self, side: Side) -> &Option<Box<AVLNode<T>>> {
        match side {
            Side::Left => &self.left,
            Side::Right => &self.right,
        }
    }

    /// Returns a mutable reference to the left or right child.
    fn child_mut(&mut self, side: Side) -> &mut Option<Box<AVLNode<T>>> {
        match side {
            Side::Left => &mut self.left,
            Side::Right => &mut self.right,
        }
    }

    /// Returns the height of the left or right subtree.
    fn height(&self, side: Side) -> usize {
        self.child(side).as_ref().map_or(0, |n| n.height)
    }

    /// Returns the height difference between the left and right subtrees.
    fn balance_factor(&self) -> i8 {
        let (left, right) = (self.height(Side::Left), self.height(Side::Right));
        if left < right {
            (right - left) as i8
        } else {
            -((left - right) as i8)
        }
    }

    /// Recomputes the `height` field.
    fn update_height(&mut self) {
        self.height = 1 + max(self.height(Side::Left), self.height(Side::Right));
    }

    /// Performs a left or right rotation.
    fn rotate(&mut self, side: Side) {
        let mut subtree = self.child_mut(!side).take().unwrap();
        *self.child_mut(!side) = subtree.child_mut(side).take();
        self.update_height();
        // Swap root and child nodes in memory
        mem::swap(self, subtree.as_mut());
        // Set old root (subtree) as child of new root (self)
        *self.child_mut(side) = Some(subtree);
        self.update_height();
    }

    /// Performs left or right tree rotations to balance this node.
    fn rebalance(&mut self) {
        self.update_height();
        let side = match self.balance_factor() {
            -2 => Side::Left,
            2 => Side::Right,
            _ => return,
        };
        let subtree = self.child_mut(side).as_mut().unwrap();
        // Left-Right and Right-Left require rotation of heavy subtree
        if let (Side::Left, 1) | (Side::Right, -1) = (side, subtree.balance_factor()) {
            subtree.rotate(side);
        }
        // Rotate in opposite direction of heavy side
        self.rotate(!side);
    }
}

impl<T: Ord> Default for AVLTree<T> {
    fn default() -> Self {
        Self::new()
    }
}

impl Not for Side {
    type Output = Side;

    fn not(self) -> Self::Output {
        match self {
            Side::Left => Side::Right,
            Side::Right => Side::Left,
        }
    }
}

impl<T: Ord> FromIterator<T> for AVLTree<T> {
    fn from_iter<I: IntoIterator<Item = T>>(iter: I) -> Self {
        let mut tree = AVLTree::new();
        for value in iter {
            tree.insert(value);
        }
        tree
    }
}

/// An iterator over the nodes of an `AVLTree`.
///
/// This struct is created by the `node_iter` method of `AVLTree`.
struct NodeIter<'a, T: Ord> {
    stack: Vec<&'a AVLNode<T>>,
}

impl<'a, T: Ord> Iterator for NodeIter<'a, T> {
    type Item = &'a AVLNode<T>;

    fn next(&mut self) -> Option<Self::Item> {
        if let Some(node) = self.stack.pop() {
            // Push left path of right subtree to stack
            let mut child = &node.right;
            while let Some(subtree) = child {
                self.stack.push(subtree.as_ref());
                child = &subtree.left;
            }
            Some(node)
        } else {
            None
        }
    }
}

/// An iterator over the items of an `AVLTree`.
///
/// This struct is created by the `iter` method of `AVLTree`.
pub struct Iter<'a, T: Ord> {
    node_iter: NodeIter<'a, T>,
}

impl<'a, T: Ord> Iterator for Iter<'a, T> {
    type Item = &'a T;

    fn next(&mut self) -> Option<&'a T> {
        match self.node_iter.next() {
            Some(node) => Some(&node.value),
            None => None,
        }
    }
}

#[cfg(test)]
mod tests {
    use super::AVLTree;

    /// Returns `true` if all nodes in the tree are balanced.
    fn is_balanced<T: Ord>(tree: &AVLTree<T>) -> bool {
        tree.node_iter()
            .all(|n| (-1..=1).contains(&n.balance_factor()))
    }

    #[test]
    fn len() {
        let tree: AVLTree<_> = (1..4).collect();
        assert_eq!(tree.len(), 3);
    }

    #[test]
    fn contains() {
        let tree: AVLTree<_> = (1..4).collect();
        assert!(tree.contains(&1));
        assert!(!tree.contains(&4));
    }

    #[test]
    fn insert() {
        let mut tree = AVLTree::new();
        // First insert succeeds
        assert!(tree.insert(1));
        // Second insert fails
        assert!(!tree.insert(1));
    }

    #[test]
    fn remove() {
        let mut tree: AVLTree<_> = (1..8).collect();
        // First remove succeeds
        assert!(tree.remove(&4));
        // Second remove fails
        assert!(!tree.remove(&4));
    }

    #[test]
    fn sorted() {
        let tree: AVLTree<_> = (1..8).rev().collect();
        assert!((1..8).eq(tree.iter().map(|&x| x)));
    }

    #[test]
    fn balanced() {
        let mut tree: AVLTree<_> = (1..8).collect();
        assert!(is_balanced(&tree));
        for x in 1..8 {
            tree.remove(&x);
            assert!(is_balanced(&tree));
        }
    }
}
}

链表

A linked list is also a linear data structure, and each element in the linked list is actually a separate object while all the objects are linked together by the reference filed in each element. In a doubly linked list, each node contains, besides the next node link, a second link field pointing to the previous node in the sequence. The two links may be called next and prev. And many modern operating systems use doubly linked lists to maintain references to active processes, threads and other dynamic objects.

Properties

• Indexing O(n)
• Insertion O(1)
  • Beginning O(1)
  • Middle (Indexing time+O(1))
  • End O(n)
• Deletion O(1)
  • Beginning O(1)
  • Middle (Indexing time+O(1))
  • End O(n)
• Search O(n)

#![allow(unused)]
fn main() {
use std::fmt::{self, Display, Formatter};
use std::ptr::NonNull;

struct Node<T> {
    val: T,
    next: Option<NonNull<Node<T>>>,
    prev: Option<NonNull<Node<T>>>,
}

impl<T> Node<T> {
    fn new(t: T) -> Node<T> {
        Node {
            val: t,
            prev: None,
            next: None,
        }
    }
}

pub struct LinkedList<T> {
    length: u32,
    start: Option<NonNull<Node<T>>>,
    end: Option<NonNull<Node<T>>>,
}

impl<T> Default for LinkedList<T> {
    fn default() -> Self {
        Self::new()
    }
}

impl<T> LinkedList<T> {
    pub fn new() -> Self {
        Self {
            length: 0,
            start: None,
            end: None,
        }
    }

    pub fn add(&mut self, obj: T) {
        let mut node = Box::new(Node::new(obj));
        // Since we are adding node at the end, next will always be None
        node.next = None;
        node.prev = self.end;
        // Get a pointer to node
        let node_ptr = Some(unsafe { NonNull::new_unchecked(Box::into_raw(node)) });
        match self.end {
            // This is the case of empty list
            None => self.start = node_ptr,
            Some(end_ptr) => unsafe { (*end_ptr.as_ptr()).next = node_ptr },
        }
        self.end = node_ptr;
        self.length += 1;
    }

    pub fn get(&mut self, index: i32) -> Option<&T> {
        self.get_ith_node(self.start, index)
    }

    fn get_ith_node(&mut self, node: Option<NonNull<Node<T>>>, index: i32) -> Option<&T> {
        match node {
            None => None,
            Some(next_ptr) => match index {
                0 => Some(unsafe { &(*next_ptr.as_ptr()).val }),
                _ => self.get_ith_node(unsafe { (*next_ptr.as_ptr()).next }, index - 1),
            },
        }
    }
}

impl<T> Display for LinkedList<T>
where
    T: Display,
{
    fn fmt(&self, f: &mut Formatter) -> fmt::Result {
        match self.start {
            Some(node) => write!(f, "{}", unsafe { node.as_ref() }),
            None => Ok(()),
        }
    }
}

impl<T> Display for Node<T>
where
    T: Display,
{
    fn fmt(&self, f: &mut Formatter) -> fmt::Result {
        match self.next {
            Some(node) => write!(f, "{}, {}", self.val, unsafe { node.as_ref() }),
            None => write!(f, "{}", self.val),
        }
    }
}

#[cfg(test)]
mod tests {
    use super::LinkedList;

    #[test]
    fn create_numeric_list() {
        let mut list = LinkedList::<i32>::new();
        list.add(1);
        list.add(2);
        list.add(3);
        println!("Linked List is {}", list);
        assert_eq!(3, list.length);
    }

    #[test]
    fn create_string_list() {
        let mut list_str = LinkedList::<String>::new();
        list_str.add("A".to_string());
        list_str.add("B".to_string());
        list_str.add("C".to_string());
        println!("Linked List is {}", list_str);
        assert_eq!(3, list_str.length);
    }

    #[test]
    fn get_by_index_in_numeric_list() {
        let mut list = LinkedList::<i32>::new();
        list.add(1);
        list.add(2);
        println!("Linked List is {}", list);
        let retrived_item = list.get(1);
        assert!(retrived_item.is_some());
        assert_eq!(2 as i32, *retrived_item.unwrap());
    }

    #[test]
    fn get_by_index_in_string_list() {
        let mut list_str = LinkedList::<String>::new();
        list_str.add("A".to_string());
        list_str.add("B".to_string());
        println!("Linked List is {}", list_str);
        let retrived_item = list_str.get(1);
        assert!(retrived_item.is_some());
        assert_eq!("B", *retrived_item.unwrap());
    }
}
}

堆(Heap)

#![allow(unused)]
fn main() {
// Heap data structure
// Takes a closure as a comparator to allow for min-heap, max-heap, and works with custom key functions

use std::cmp::Ord;
use std::default::Default;

pub struct Heap<T>
where
    T: Default,
{
    count: usize,
    items: Vec<T>,
    comparator: fn(&T, &T) -> bool,
}

impl<T> Heap<T>
where
    T: Default,
{
    pub fn new(comparator: fn(&T, &T) -> bool) -> Self {
        Self {
            count: 0,
            // Add a default in the first spot to offset indexes
            // for the parent/child math to work out.
            // Vecs have to have all the same type so using Default
            // is a way to add an unused item.
            items: vec![T::default()],
            comparator,
        }
    }

    pub fn len(&self) -> usize {
        self.count
    }

    pub fn is_empty(&self) -> bool {
        self.len() == 0
    }

    pub fn add(&mut self, value: T) {
        self.count += 1;
        self.items.push(value);

        // Heapify Up
        let mut idx = self.count;
        while self.parent_idx(idx) > 0 {
            let pdx = self.parent_idx(idx);
            if (self.comparator)(&self.items[idx], &self.items[pdx]) {
                self.items.swap(idx, pdx);
            }
            idx = pdx;
        }
    }

    fn parent_idx(&self, idx: usize) -> usize {
        idx / 2
    }

    fn children_present(&self, idx: usize) -> bool {
        self.left_child_idx(idx) <= self.count
    }

    fn left_child_idx(&self, idx: usize) -> usize {
        idx * 2
    }

    fn right_child_idx(&self, idx: usize) -> usize {
        self.left_child_idx(idx) + 1
    }

    fn smallest_child_idx(&self, idx: usize) -> usize {
        if self.right_child_idx(idx) > self.count {
            self.left_child_idx(idx)
        } else {
            let ldx = self.left_child_idx(idx);
            let rdx = self.right_child_idx(idx);
            if (self.comparator)(&self.items[ldx], &self.items[rdx]) {
                ldx
            } else {
                rdx
            }
        }
    }
}

impl<T> Heap<T>
where
    T: Default + Ord,
{
    /// Create a new MinHeap
    pub fn new_min() -> Self {
        Self::new(|a, b| a < b)
    }

    /// Create a new MaxHeap
    pub fn new_max() -> Self {
        Self::new(|a, b| a > b)
    }
}

impl<T> Iterator for Heap<T>
where
    T: Default,
{
    type Item = T;

    fn next(&mut self) -> Option<T> {
        if self.count == 0 {
            return None;
        }
        // This feels like a function built for heap impl :)
        // Removes an item at an index and fills in with the last item
        // of the Vec
        let next = Some(self.items.swap_remove(1));
        self.count -= 1;

        if self.count > 0 {
            // Heapify Down
            let mut idx = 1;
            while self.children_present(idx) {
                let cdx = self.smallest_child_idx(idx);
                if !(self.comparator)(&self.items[idx], &self.items[cdx]) {
                    self.items.swap(idx, cdx);
                }
                idx = cdx;
            }
        }

        next
    }
}

pub struct MinHeap;

impl MinHeap {
    #[allow(clippy::new_ret_no_self)]
    pub fn new<T>() -> Heap<T>
    where
        T: Default + Ord,
    {
        Heap::new(|a, b| a < b)
    }
}

pub struct MaxHeap;

impl MaxHeap {
    #[allow(clippy::new_ret_no_self)]
    pub fn new<T>() -> Heap<T>
    where
        T: Default + Ord,
    {
        Heap::new(|a, b| a > b)
    }
}

#[cfg(test)]
mod tests {
    use super::*;
    #[test]
    fn test_empty_heap() {
        let mut heap = MaxHeap::new::<i32>();
        assert_eq!(heap.next(), None);
    }

    #[test]
    fn test_min_heap() {
        let mut heap = MinHeap::new();
        heap.add(4);
        heap.add(2);
        heap.add(9);
        heap.add(11);
        assert_eq!(heap.len(), 4);
        assert_eq!(heap.next(), Some(2));
        assert_eq!(heap.next(), Some(4));
        assert_eq!(heap.next(), Some(9));
        heap.add(1);
        assert_eq!(heap.next(), Some(1));
    }

    #[test]
    fn test_max_heap() {
        let mut heap = MaxHeap::new();
        heap.add(4);
        heap.add(2);
        heap.add(9);
        heap.add(11);
        assert_eq!(heap.len(), 4);
        assert_eq!(heap.next(), Some(11));
        assert_eq!(heap.next(), Some(9));
        assert_eq!(heap.next(), Some(4));
        heap.add(1);
        assert_eq!(heap.next(), Some(2));
    }

    struct Point(/* x */ i32, /* y */ i32);
    impl Default for Point {
        fn default() -> Self {
            Self(0, 0)
        }
    }

    #[test]
    fn test_key_heap() {
        let mut heap: Heap<Point> = Heap::new(|a, b| a.0 < b.0);
        heap.add(Point(1, 5));
        heap.add(Point(3, 10));
        heap.add(Point(-2, 4));
        assert_eq!(heap.len(), 3);
        assert_eq!(heap.next().unwrap().0, -2);
        assert_eq!(heap.next().unwrap().0, 1);
        heap.add(Point(50, 34));
        assert_eq!(heap.next().unwrap().0, 3);
    }
}
}

栈

From Wikipedia, a stack is an abstract data type that serves as a collection of elements, with two main principal operations, Push and Pop.

Properties

• Push O(1)
• Pop head.data O(1) tail.data O(n)
• Peek O(1)

// the public struct can hide the implementation detail
pub struct Stack<T> {
    head: Link<T>,
}

type Link<T> = Option<Box<Node<T>>>;

struct Node<T> {
    elem: T,
    next: Link<T>,
}

impl<T> Stack<T> {
    // Self is an alias for Stack
    // We implement associated function name new for single-linked-list
    pub fn new() -> Self {
        // for new function we need to return a new instance
        Self {
            // we refer to variants of an enum using :: the namespacing operator
            head: None,
        } // we need to return the variant, so there without the ;
    }

    // As we know the primary forms that self can take: self, &mut self and &self, push will change the linked list
    // so we need &mut
    // The push method which the signature's first parameter is self
    pub fn push(&mut self, elem: T) {
        let new_node = Box::new(Node {
            elem,
            next: self.head.take(),
        });
        // don't forget replace the head with new node for stack
        self.head = Some(new_node);
    }
    ///
    /// In pop function, we trying to:
    /// * check if the list is empty, so we use enum Option<T>, it can either be Some(T) or None
    ///   * if it's empty, return None
    ///   * if it's not empty
    ///     * remove the head of the list
    ///     * remove its elem
    ///     * replace the list's head with its next
    ///     * return Some(elem), as the situation if need
    ///
    /// so, we need to remove the head, and return the value of the head
    pub fn pop(&mut self) -> Result<T, &str> {
        match self.head.take() {
            None => Err("Stack is empty"),
            Some(node) => {
                self.head = node.next;
                Ok(node.elem)
            }
        }
    }

    pub fn is_empty(&self) -> bool {
        // Returns true if the option is a [None] value.
        self.head.is_none()
    }

    pub fn peek(&self) -> Option<&T> {
        // Converts from &Option<T> to Option<&T>.
        match self.head.as_ref() {
            None => None,
            Some(node) => Some(&node.elem),
        }
    }

    pub fn peek_mut(&mut self) -> Option<&mut T> {
        match self.head.as_mut() {
            None => None,
            Some(node) => Some(&mut node.elem),
        }
    }

    pub fn into_iter_for_stack(self) -> IntoIter<T> {
        IntoIter(self)
    }
    pub fn iter(&self) -> Iter<'_, T> {
        Iter {
            next: self.head.as_deref(),
        }
    }
    // '_ is the "explicitly elided lifetime" syntax of Rust
    pub fn iter_mut(&mut self) -> IterMut<'_, T> {
        IterMut {
            next: self.head.as_deref_mut(),
        }
    }
}

impl<T> Default for Stack<T> {
    fn default() -> Self {
        Self::new()
    }
}

/// The drop method of singly linked list. There's a question that do we need to worry about cleaning up our list?
/// As we all know the ownership and borrow mechanism, so we know the type will clean automatically after it goes out the scope,
/// this implement by the Rust compiler automatically did which mean add trait `drop` for the automatically.
///
/// So, the complier will implements Drop for `List->Link->Box<Node> ->Node` automatically and tail recursive to clean the elements
/// one by one. And we know the recursive will stop at Box<Node>
/// https://rust-unofficial.github.io/too-many-lists/first-drop.html
///
/// As we know we can't drop the contents of the Box after deallocating, so we need to manually write the iterative drop

impl<T> Drop for Stack<T> {
    fn drop(&mut self) {
        let mut cur_link = self.head.take();
        while let Some(mut boxed_node) = cur_link {
            cur_link = boxed_node.next.take();
            // boxed_node goes out of scope and gets dropped here;
            // but its Node's `next` field has been set to None
            // so no unbound recursion occurs.
        }
    }
}

/// Rust has nothing like a yield statement, and there's actually 3 different kinds of iterator should to implement

// Collections are iterated in Rust using the Iterator trait, we define a struct implement Iterator
pub struct IntoIter<T>(Stack<T>);

impl<T> Iterator for IntoIter<T> {
    // This is declaring that every implementation of iterator has an associated type called Item
    type Item = T;
    // the reason iterator yield Option<self::Item> is because the interface coalesces the `has_next` and `get_next` concepts
    fn next(&mut self) -> Option<Self::Item> {
        self.0.pop().ok()
    }
}

pub struct Iter<'a, T> {
    next: Option<&'a Node<T>>,
}

impl<'a, T> Iterator for Iter<'a, T> {
    type Item = &'a T;
    fn next(&mut self) -> Option<Self::Item> {
        self.next.map(|node| {
            // as_deref: Converts from Option<T> (or &Option<T>) to Option<&T::Target>.
            self.next = node.next.as_deref();
            &node.elem
        })
    }
}

pub struct IterMut<'a, T> {
    next: Option<&'a mut Node<T>>,
}

impl<'a, T> Iterator for IterMut<'a, T> {
    type Item = &'a mut T;
    fn next(&mut self) -> Option<Self::Item> {
        // we add take() here due to &mut self isn't Copy(& and Option<&> is Copy)
        self.next.take().map(|node| {
            self.next = node.next.as_deref_mut();
            &mut node.elem
        })
    }
}

#[cfg(test)]
mod test_stack {

    use super::*;

    #[test]
    fn basics() {
        let mut list = Stack::new();
        assert_eq!(list.pop(), Err("Stack is empty"));

        list.push(1);
        list.push(2);
        list.push(3);

        assert_eq!(list.pop(), Ok(3));
        assert_eq!(list.pop(), Ok(2));

        list.push(4);
        list.push(5);

        assert_eq!(list.is_empty(), false);

        assert_eq!(list.pop(), Ok(5));
        assert_eq!(list.pop(), Ok(4));

        assert_eq!(list.pop(), Ok(1));
        assert_eq!(list.pop(), Err("Stack is empty"));

        assert_eq!(list.is_empty(), true);
    }

    #[test]
    fn peek() {
        let mut list = Stack::new();
        assert_eq!(list.peek(), None);
        list.push(1);
        list.push(2);
        list.push(3);

        assert_eq!(list.peek(), Some(&3));
        assert_eq!(list.peek_mut(), Some(&mut 3));

        match list.peek_mut() {
            None => None,
            Some(value) => Some(*value = 42),
        };

        assert_eq!(list.peek(), Some(&42));
        assert_eq!(list.pop(), Ok(42));
    }

    #[test]
    fn into_iter() {
        let mut list = Stack::new();
        list.push(1);
        list.push(2);
        list.push(3);

        let mut iter = list.into_iter_for_stack();
        assert_eq!(iter.next(), Some(3));
        assert_eq!(iter.next(), Some(2));
        assert_eq!(iter.next(), Some(1));
        assert_eq!(iter.next(), None);
    }

    #[test]
    fn iter() {
        let mut list = Stack::new();
        list.push(1);
        list.push(2);
        list.push(3);

        let mut iter = list.iter();
        assert_eq!(iter.next(), Some(&3));
        assert_eq!(iter.next(), Some(&2));
        assert_eq!(iter.next(), Some(&1));
    }

    #[test]
    fn iter_mut() {
        let mut list = Stack::new();
        list.push(1);
        list.push(2);
        list.push(3);

        let mut iter = list.iter_mut();
        assert_eq!(iter.next(), Some(&mut 3));
        assert_eq!(iter.next(), Some(&mut 2));
        assert_eq!(iter.next(), Some(&mut 1));
    }
}

队列

#![allow(unused)]
fn main() {
#[derive(Debug)]
pub struct Queue<T> {
    elements: Vec<T>,
}

impl<T: Clone> Queue<T> {
    pub fn new() -> Queue<T> {
        Queue {
            elements: Vec::new(),
        }
    }

    pub fn enqueue(&mut self, value: T) {
        self.elements.push(value)
    }

    pub fn dequeue(&mut self) -> Result<T, &str> {
        if !self.elements.is_empty() {
            Ok(self.elements.remove(0usize))
        } else {
            Err("Queue is empty")
        }
    }

    pub fn peek(&self) -> Result<&T, &str> {
        match self.elements.first() {
            Some(value) => Ok(value),
            None => Err("Queue is empty"),
        }
    }

    pub fn size(&self) -> usize {
        self.elements.len()
    }

    pub fn is_empty(&self) -> bool {
        self.elements.is_empty()
    }
}

impl<T> Default for Queue<T> {
    fn default() -> Queue<T> {
        Queue {
            elements: Vec::new(),
        }
    }
}

#[cfg(test)]
mod tests {
    use super::Queue;

    #[test]
    fn test_enqueue() {
        let mut queue: Queue<u8> = Queue::new();
        queue.enqueue(64);
        assert_eq!(queue.is_empty(), false);
    }

    #[test]
    fn test_dequeue() {
        let mut queue: Queue<u8> = Queue::new();
        queue.enqueue(32);
        queue.enqueue(64);
        let retrieved_dequeue = queue.dequeue();
        assert!(retrieved_dequeue.is_ok());
        assert_eq!(32, retrieved_dequeue.unwrap());
    }

    #[test]
    fn test_peek() {
        let mut queue: Queue<u8> = Queue::new();
        queue.enqueue(8);
        queue.enqueue(16);
        let retrieved_peek = queue.peek();
        assert!(retrieved_peek.is_ok());
        assert_eq!(8, *retrieved_peek.unwrap());
    }

    #[test]
    fn test_size() {
        let mut queue: Queue<u8> = Queue::new();
        queue.enqueue(8);
        queue.enqueue(16);
        assert_eq!(2, queue.size());
    }
}
}

trie树

#![allow(unused)]
fn main() {
use std::collections::HashMap;
use std::hash::Hash;

#[derive(Debug, Default)]
struct Node<Key: Default, Type: Default> {
    children: HashMap<Key, Node<Key, Type>>,
    value: Option<Type>,
}

#[derive(Debug, Default)]
pub struct Trie<Key, Type>
where
    Key: Default + Eq + Hash,
    Type: Default,
{
    root: Node<Key, Type>,
}

impl<Key, Type> Trie<Key, Type>
where
    Key: Default + Eq + Hash,
    Type: Default,
{
    pub fn new() -> Self {
        Self {
            root: Node::default(),
        }
    }

    pub fn insert(&mut self, key: impl IntoIterator<Item = Key>, value: Type)
    where
        Key: Eq + Hash,
    {
        let mut node = &mut self.root;
        for c in key.into_iter() {
            node = node.children.entry(c).or_insert_with(Node::default);
        }
        node.value = Some(value);
    }

    pub fn get(&self, key: impl IntoIterator<Item = Key>) -> Option<&Type>
    where
        Key: Eq + Hash,
    {
        let mut node = &self.root;
        for c in key.into_iter() {
            if node.children.contains_key(&c) {
                node = node.children.get(&c).unwrap()
            } else {
                return None;
            }
        }
        node.value.as_ref()
    }
}

#[cfg(test)]
mod tests {

    use super::*;

    #[test]
    fn test_insertion() {
        let mut trie = Trie::new();
        assert_eq!(trie.get("".chars()), None);

        trie.insert("foo".chars(), 1);
        trie.insert("foobar".chars(), 2);

        let mut trie = Trie::new();
        assert_eq!(trie.get(vec![1, 2, 3]), None);

        trie.insert(vec![1, 2, 3], 1);
        trie.insert(vec![3, 4, 5], 2);
    }

    #[test]
    fn test_get() {
        let mut trie = Trie::new();
        trie.insert("foo".chars(), 1);
        trie.insert("foobar".chars(), 2);
        trie.insert("bar".chars(), 3);
        trie.insert("baz".chars(), 4);

        assert_eq!(trie.get("foo".chars()), Some(&1));
        assert_eq!(trie.get("food".chars()), None);

        let mut trie = Trie::new();
        trie.insert(vec![1, 2, 3, 4], 1);
        trie.insert(vec![42], 2);
        trie.insert(vec![42, 6, 1000], 3);
        trie.insert(vec![1, 2, 4, 16, 32], 4);

        assert_eq!(trie.get(vec![42, 6, 1000]), Some(&3));
        assert_eq!(trie.get(vec![43, 44, 45]), None);
    }
}
}

图(graph)

#![allow(unused)]
fn main() {
use std::collections::{HashMap, HashSet};
use std::fmt;

#[derive(Debug, Clone)]
pub struct NodeNotInGraph;

impl fmt::Display for NodeNotInGraph {
    fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result {
        write!(f, "accessing a node that is not in the graph")
    }
}

pub struct DirectedGraph {
    adjacency_table: HashMap<String, Vec<(String, i32)>>,
}

impl Graph for DirectedGraph {
    fn new() -> DirectedGraph {
        DirectedGraph {
            adjacency_table: HashMap::new(),
        }
    }
    fn adjacency_table_mutable(&mut self) -> &mut HashMap<String, Vec<(String, i32)>> {
        &mut self.adjacency_table
    }
    fn adjacency_table(&self) -> &HashMap<String, Vec<(String, i32)>> {
        &self.adjacency_table
    }
}

pub struct UndirectedGraph {
    adjacency_table: HashMap<String, Vec<(String, i32)>>,
}

impl Graph for UndirectedGraph {
    fn new() -> UndirectedGraph {
        UndirectedGraph {
            adjacency_table: HashMap::new(),
        }
    }
    fn adjacency_table_mutable(&mut self) -> &mut HashMap<String, Vec<(String, i32)>> {
        &mut self.adjacency_table
    }
    fn adjacency_table(&self) -> &HashMap<String, Vec<(String, i32)>> {
        &self.adjacency_table
    }
    fn add_edge(&mut self, edge: (&str, &str, i32)) {
        self.add_node(edge.0);
        self.add_node(edge.1);

        self.adjacency_table
            .entry(edge.0.to_string())
            .and_modify(|e| {
                e.push((edge.1.to_string(), edge.2));
            });
        self.adjacency_table
            .entry(edge.1.to_string())
            .and_modify(|e| {
                e.push((edge.0.to_string(), edge.2));
            });
    }
}

pub trait Graph {
    fn new() -> Self;
    fn adjacency_table_mutable(&mut self) -> &mut HashMap<String, Vec<(String, i32)>>;
    fn adjacency_table(&self) -> &HashMap<String, Vec<(String, i32)>>;

    fn add_node(&mut self, node: &str) -> bool {
        match self.adjacency_table().get(node) {
            None => {
                self.adjacency_table_mutable()
                    .insert((*node).to_string(), Vec::new());
                true
            }
            _ => false,
        }
    }

    fn add_edge(&mut self, edge: (&str, &str, i32)) {
        self.add_node(edge.0);
        self.add_node(edge.1);

        self.adjacency_table_mutable()
            .entry(edge.0.to_string())
            .and_modify(|e| {
                e.push((edge.1.to_string(), edge.2));
            });
    }

    fn neighbours(&self, node: &str) -> Result<&Vec<(String, i32)>, NodeNotInGraph> {
        match self.adjacency_table().get(node) {
            None => Err(NodeNotInGraph),
            Some(i) => Ok(i),
        }
    }

    fn contains(&self, node: &str) -> bool {
        self.adjacency_table().get(node).is_some()
    }

    fn nodes(&self) -> HashSet<&String> {
        self.adjacency_table().keys().collect()
    }

    fn edges(&self) -> Vec<(&String, &String, i32)> {
        let mut edges = Vec::new();
        for (from_node, from_node_neighbours) in self.adjacency_table() {
            for (to_node, weight) in from_node_neighbours {
                edges.push((from_node, to_node, *weight));
            }
        }
        edges
    }
}

#[cfg(test)]
mod test_undirected_graph {
    use super::Graph;
    use super::UndirectedGraph;
    #[test]
    fn test_add_edge() {
        let mut graph = UndirectedGraph::new();

        graph.add_edge(("a", "b", 5));
        graph.add_edge(("b", "c", 10));
        graph.add_edge(("c", "a", 7));

        let expected_edges = [
            (&String::from("a"), &String::from("b"), 5),
            (&String::from("b"), &String::from("a"), 5),
            (&String::from("c"), &String::from("a"), 7),
            (&String::from("a"), &String::from("c"), 7),
            (&String::from("b"), &String::from("c"), 10),
            (&String::from("c"), &String::from("b"), 10),
        ];
        for edge in expected_edges.iter() {
            assert_eq!(graph.edges().contains(edge), true);
        }
    }

    #[test]
    fn test_neighbours() {
        let mut graph = UndirectedGraph::new();

        graph.add_edge(("a", "b", 5));
        graph.add_edge(("b", "c", 10));
        graph.add_edge(("c", "a", 7));

        assert_eq!(
            graph.neighbours("a").unwrap(),
            &vec![(String::from("b"), 5), (String::from("c"), 7)]
        );
    }
}

#[cfg(test)]
mod test_directed_graph {
    use super::DirectedGraph;
    use super::Graph;

    #[test]
    fn test_add_node() {
        let mut graph = DirectedGraph::new();
        graph.add_node("a");
        graph.add_node("b");
        graph.add_node("c");
        assert_eq!(
            graph.nodes(),
            [&String::from("a"), &String::from("b"), &String::from("c")]
                .iter()
                .cloned()
                .collect()
        );
    }

    #[test]
    fn test_add_edge() {
        let mut graph = DirectedGraph::new();

        graph.add_edge(("a", "b", 5));
        graph.add_edge(("c", "a", 7));
        graph.add_edge(("b", "c", 10));

        let expected_edges = [
            (&String::from("a"), &String::from("b"), 5),
            (&String::from("c"), &String::from("a"), 7),
            (&String::from("b"), &String::from("c"), 10),
        ];
        for edge in expected_edges.iter() {
            assert_eq!(graph.edges().contains(edge), true);
        }
    }

    #[test]
    fn test_neighbours() {
        let mut graph = DirectedGraph::new();

        graph.add_edge(("a", "b", 5));
        graph.add_edge(("b", "c", 10));
        graph.add_edge(("c", "a", 7));

        assert_eq!(
            graph.neighbours("a").unwrap(),
            &vec![(String::from("b"), 5)]
        );
    }

    #[test]
    fn test_contains() {
        let mut graph = DirectedGraph::new();
        graph.add_node("a");
        graph.add_node("b");
        graph.add_node("c");
        assert_eq!(graph.contains("a"), true);
        assert_eq!(graph.contains("b"), true);
        assert_eq!(graph.contains("c"), true);
        assert_eq!(graph.contains("d"), false);
    }
}
}

LeetCode题解

目前网上用Rust刷LeetCode的题解相对较少且很少有详细解释，为此在这本算法书里我们希望能够打破这一僵局，写出一份让每个人都能看懂的LeetCode题解。暂定计划按题号顺序来，每日一题，尽可能做到每一题都附带详细过程，如有不足之处，也欢迎大家指出和提出PR。

1. 两数之和

题目链接: 两数之和

相信每个刷过LeetCode的人永远也忘不了这道题（就想当年背单词书永远也忘不了书中的第一个单词abandon哈哈哈），但是这道题用Rust来写也并不是那么简单，尤其是对于Rust新手，相信看完这道题你对Rust中的一些小细节会有更深的理解。

解法一

简单粗暴，双重循环，遍历所有的二元组直到找到符合题目要求的结果。

#![allow(unused)]
fn main() {
impl Solution {
    pub fn two_sum(nums: Vec<i32>, target: i32) -> Vec<i32> {
        for i in 0..nums.len() {
            for j in (i + 1)..nums.len() {
                if nums[i] + nums[j] == target {
                    // 注意Rust中下标索引类型为usize，因此这里我们需要将i, j转换为i32
                    return vec![i as i32, j as i32];
                }
            }
        }
        vec![]
    }
}
}

解法二

我们观察解法一中第二个for循环：

#![allow(unused)]
fn main() {
for j in (i + 1)..nums.len() {
    if nums[i] + nums[j] == target {
        ...
    }
}
}

我们换种方式思考：

#![allow(unused)]
fn main() {
for j in (i + 1)..nums.len() {
    let other = target - nums[i];
    if nums[j] == other {
        ...
    }
}
}

因此我们的目标就变成了在一个数组中寻找值，这可是HashSet/HashMap的强项啊！由于这里我们还需要获取到对应值在数组中的下标索引位置，因此这里只能用HashMap了。

#![allow(unused)]
fn main() {
use std::collections::HashMap;

impl Solution {
    pub fn two_sum(nums: Vec<i32>, target: i32) -> Vec<i32> {
        let mut map = HashMap::new();
        for (index, value) in nums.iter().enumerate() {
            let other = target - value;
            if let Some(&other_index) = map.get(&other) {
                return vec![other_index as i32, index as i32];
            }
            map.insert(value, index);
        }
        vec![]
    }
}
}

如果你是个Rust新手的话，相信你可能会存在以下几点疑惑：

• 为什么需要use std::collections::HashMap;这一行：可能是觉得HashMap用的没有那么多吧，因此Rust并没有将HashMap列入Prelude行列当中，因此当我们需要使用HashMap时，需要手动引入。
• 前面的for i in 0..nums.len()哪去了，这个for (index, value) in nums.iter().enumerate()是个什么鬼：在Rust中推荐使用迭代器，而enumerate这个迭代器适配器返回含有(下标，值)的元组。
• 为什么if let Some(&other_index) = map.get(&other)需要用到两个引用符号：简单来说，因为所有权的问题。HashMap的get方法中传入的参数是对key的引用，返回的是Option<&value>，因此我们需要用这两个引用符号。